Question

【题目】如图，点A、B、C在同一直线上，△ABD，△BCE都是等边三角形．

（1）求证：AE=CD；

（2）若M，N分别是AE，CD的中点，试判断△BMN的形状，并证明你的结论．

Answer 1

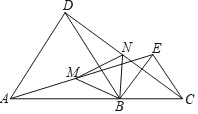
【答案】（1）答案见解析；（2）△MBN是等边三角形．

【解析】整体分析：

(1)利用SAS证明△AOC≌△BOD，则有AE＝CD；(2)由△ABE≌△DBC，可证△ABM≌△DBN，从而得BM＝BN，∠MBN＝60°.

(1)证明：∵△ABD、△BCE都是等边三角形，

∴AB＝BD，BC＝BE，∠ABD＝∠CBE＝60°，

∴∠ABD＋∠DBE＝∠DBE＋∠CBE即∠ABE＝∠DBC，

∴在△ABE和△DBC中，

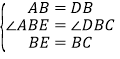
△ABE≌△DBC(SAS)．

∴AE＝CD．

(2)解：△MBN是等边三角形，理由如下：

∵△ABE≌△DBC，

∴∠BAE＝∠BDC．

∵AE＝CD，M、N分别是AE、CD的中点，

∴AM＝DN；

又∵AB＝DB．

∴△ABM≌△DBN．

BM＝BN．

∠ABM＝∠DBN．

∴∠DBM＋∠DBN＝∠DBM＋∠ABM＝∠ABD＝60°．

∴△MBN是等边三角形．