题目内容
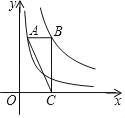
【题目】如图,点A与点B在反比例函数y=![]() (x>0)的图象上,A点的纵坐标为2,BB′与AA′均垂直于x轴,B′,A′是垂足.
(x>0)的图象上,A点的纵坐标为2,BB′与AA′均垂直于x轴,B′,A′是垂足.
(1)求A点的坐标;
(2)求△BOB′的面积;
(3)若B点的横坐标为2,求△OAB的面积.
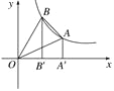
【答案】(1) (4,2);(2) 4;(3)6.
【解析】
(1)把y=2代入函数解析式即可求得A的横坐标即可求得A的坐标;
(2)根据反比例函数的解析式的意义即可求得三角形的面积;
(3)根据△AOB的面积=△OBB'的面积+S梯形OA'AB的面积-△OAA'的面积求解.
解:(1)当y=2时,则x=![]() =4.即点A的坐标是(4,2);
=4.即点A的坐标是(4,2);
(2)S△BOB′=![]() ×8=4;
×8=4;
(3)在y=![]() 中,当x=2时,y=
中,当x=2时,y=![]() =4,则B的坐标是(2,4),
=4,则B的坐标是(2,4),
根据反比例函数的解析式知,三角形OAA′的面积和三角形OBB′的面积相等,都是4,则直角梯形ABB′A′的面积是![]() ×(2+4)×2=6.所以S△OAB=S△BOB′+S梯形SA′ABB′-S△OAA′=4+6-4
×(2+4)×2=6.所以S△OAB=S△BOB′+S梯形SA′ABB′-S△OAA′=4+6-4
=6.

练习册系列答案
相关题目