题目内容
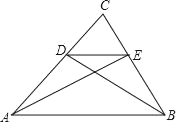
【题目】如图,点D、E分别在△ABC的边AC和BC上,∠C=90°,DE∥AB,且3DE=2AB,AE=13,BD=9,那么AB的长为_____.
【答案】![]()
【解析】分析:先设DE=2x,CD=2y,CE=2z,由于DE∥AB,3DE=2AB,根据平行线分线段成比例定理,可得AB=3x,AC=3y,BC=3z,而∠C=90°,利用勾股定理,可得y2+z2=x2①,(3y)2+(2z)2=132②,(2y)2+(3z)2=92③,解关于①②③的方程,可求x,从而可求AB.
详解:设DE=2x,CD=2y,CE=2z,
∵DE∥AB,3DE=2AB,
∴AB=3x,AC=3y,BC=3z,
又∵∠C=90°,
∴(2y)2+(2z)2=(2x)2,
即y2+z2=x2,①
同理(3y)2+(2z)2=132,②
(2y)2+(3z)2=92,③
②-①×4,得
5y2=169-4x2,④
①×9-③,得
5y2=9x2-81,⑤
⑤-④,得
x2=![]() ,
,
x=![]()
∴AB=3x=![]() .
.
故答案为:![]() .
.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
【题目】空气质量指数是国际上普遍采用的定量评价空气质量好坏的重要指标,空气质量指数不超过50则空气质量评估为优.下表记录了我市11月某一周7天的空气质量指数变化情况.规定:空气质量指数50记为零,空气质量指数超过50记为正,空气质量指数低于50记为负.
星期一 | 星期二 | 星期三 | 星期四 | 星期五 | 星期六 | 星期日 |
+18 | ﹣4 | ﹣1 | ﹣18 | ﹣10 | +28 | +29 |
解答以下问题:
(1)根据表格可知,星期四空气质量指数为 ,星期六比星期二空气质量指数高 ;
(2)求这一周7天的平均空气质量指数.