题目内容
在△ABC中，AD平分∠BAC交BC于D，EF∥AD，交AC于E，交BA的延长线于F，求证：△AEF为等腰三角形．
分析：由在△ABC中，AD平分∠BAC交BC于D，EF∥AD，易证得∠F=∠AEF，继而可证得AE=AF．
解答：证明：∵EF∥AD，
∴∠F=∠BAD，∠AEF=∠DAC．
∵AD平分∠BAC，
∴∠BAD=∠DAC，
∴∠F=∠AEF，
∴AE=AF，即△AEF为等腰三角形．
∴∠F=∠BAD，∠AEF=∠DAC．
∵AD平分∠BAC，
∴∠BAD=∠DAC，
∴∠F=∠AEF，
∴AE=AF，即△AEF为等腰三角形．
点评：此题考查了等腰三角形的判定以及平行线的性质．此题比较简单，注意掌握数形结合思想的应用．
练习册系列答案
相关题目
16、如图，在△ABC中，AD是△ABC中∠CAB的角平分钱，要使△ADC≌△ADE，需要添加一个条件，这个条件是
（2012•开平区一模）如图，△ABC中，AB＞AC，AD平分∠BAC，且交BC于点D，在AB上截取AE=AC，过点E作EF∥BC交AD于点F．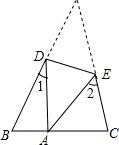
如图，在△ABC中，将∠A折叠压平，使点A落在BC上，则∠1，∠2，∠A三者之间的等量关系为（ ）
∠CAB交
BC于D，DE⊥AB于E．若DE=1cm，则BC =（ ） cm．