Question

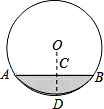
已知⊙O的半径OA=1，弦AB、AC的长分别是

2

、

3

，则∠BAC的度数是______．

Answer 1

分别作OD⊥AB，OE⊥AC，垂足分别是D、E．
∵OE⊥AC，OD⊥AB，根据垂径定理得AE=

1

2

AC=

3

2

，AD=

1

2

AB=

2

2

，
∴sin∠AOE=

AE

AO

=

3 2

1

=

3

2

，sin∠AOD=

AD

OA

=

2

2

，
根据特殊角的三角函数值可得∠AOE=60°，∠AOD=45°，
∴∠BAO=45°，∠CAO=90°-60°=30°，
∴∠BAC=45°+30°=75°，
或∠BAC′=45°-30°=15°．
故答案为：15°或75°．