Question

【题目】如图，在平面直角坐标系xOy中，直线y＝﹣x+与y＝x相交于点A，与x轴交于点B.

(1)填空：A的坐标是_______，B的坐标是___________；

(2)直线y＝﹣x+上有点P(m，n)，且点P在第四象限，设△AOP的面积为S，请求出S与m的函数关系式；

(3)在直线OA上，是否存在一点D，使得△DOB是等腰三角形？如果存在，试求出所有符合条件的点D的坐标，如果不存在，请说明理由.

Answer 1

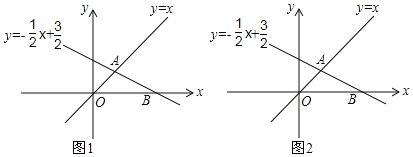
【答案】(1)A（1,1），B(3，0)；(2)S=；(3)存在，D(﹣，﹣)，D(，)，D(3，3)或D(，).

【解析】

（1）把直线y=-x+与y=x联立得出方程组求解即可得出点A的坐标，由直线y=-x+与x轴交于点B，令y=0，求出x的值，即可得出B的坐标；

（2）根据S = S△AOB+ S△POB即可解答；

（3）在直线OA上，存在一点D，使得△DOB是等腰三角形，分四种情况①当OB=OD时，②当OD=OB时，③当OB=DB时，④当DO=DB时分别求解即可．

解：(1)∵直线y＝﹣x+与y＝x相交于点A，

∴联立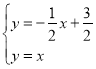得 ，解得，

∴点A(1，1)，

∵直线y＝﹣x+与x轴交于点B，

∴令y＝0，得﹣x+＝0，解得x＝3，

∴B(3，0).

(2)S=S△AOB+S△OBP=

(3)在直线OA上，存在一点D，使得△DOB是等腰三角形，

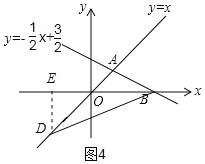
①如图4，当OB＝OD时，作DE⊥x轴，交x轴于点E

∵OB＝3，点D在OA上，∠DOE＝45°

∴DE＝OE＝，

∴D(﹣，﹣)，

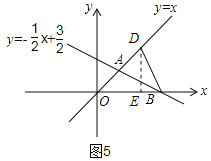
②如图5，当OD＝OB时，作DE⊥x轴，交x轴于点E

∵OB＝3，点D在OA上，∠DOE＝45°

∴DE＝OE＝，

∴D(，)，

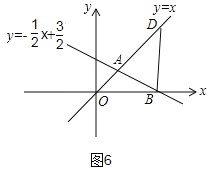
③如图6，当OB＝DB时，

∵∠AOB＝∠ODB＝45°，

∴DB⊥OB，

∵OB＝3，

∴D(3，3)，

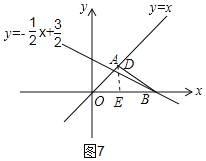
④如图7，当DO＝DB时，作DE⊥x轴，交x轴于点E

∵∠AOB＝∠OBD＝45°，

∴OD⊥DB，

∵OB＝3，

∴OE＝，AE＝，

∴D(，).

综上所述，在直线OA上，存在点D(﹣，﹣)，D(，)，D(3，3)或D(，)，使得△DOB是等腰三角形.