题目内容
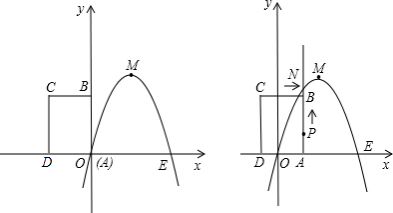
如图,已知抛物线![]() 经过A(1,0),B(0,2)两点,顶点为D.
经过A(1,0),B(0,2)两点,顶点为D.
1.求抛物线的解析式;
2.将△OAB绕点A顺时针旋转90°后,点B落到点C的位置,将抛物线沿y轴平移后经过点C,求平移后所得图像的函数关系式;
3.设(2)中平移后,所得抛物线与y轴的交点为![]() ,顶点为
,顶点为![]() ,若点N在平移后的抛物线上,且满足△
,若点N在平移后的抛物线上,且满足△![]() 的面积是△
的面积是△![]() 面积的2倍,求点N的坐标.
面积的2倍,求点N的坐标.

1.![]()
2.![]()
3.(1,-1)或(3,1).
解析:抛物线的解析式解析式的求解一般为待定系数法。注意其中的a是给了的所以两个点坐标就可以了。而问题(2)有关函数平移问题注意上下来移和C有关。
解:(1)已知抛物线![]() 经过A(1,0),B(0,2),
经过A(1,0),B(0,2),
∴![]() 解得
解得![]()
∴所求抛物线的解析式为![]() . (3分)
. (3分)
(2)∵A(1,0),B(0,2),∴OA=1,OB=2
可得旋转后C点的坐标为(3,1)
当x=3时,由 得y=2,
得y=2,
可知抛物线![]() 过点(3,2)
过点(3,2)
∴将原抛物线沿y轴向下平移1个单位后过点C.
∴平移后的抛物线解析式为:![]() . (7分)
. (7分)
(3)∵点N在![]() 上,可设N点坐标为(
上,可设N点坐标为(![]() )
)
将![]() 配方得
配方得![]() .∴其对称轴为
.∴其对称轴为![]() . 6分
. 6分
①当0< <
<![]() 时,如图①,
时,如图①,
∵S![]() =2S
=2S![]() ∴
∴![]() ∴
∴![]() =1.此时
=1.此时![]()
∴N点的坐标为(1,-1).


②当 >
>![]() 时,如图②
时,如图②
同理可得
∴ =3. 此时
=3. 此时![]()
∴点N的坐标为(3,1).
综上,点N的坐标为(1,-1)或(3,1). (13分)

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
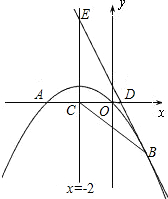 2x+1经过抛物线上一点B(2,m),且与y轴.直线x=-2分别交于点D、E.
2x+1经过抛物线上一点B(2,m),且与y轴.直线x=-2分别交于点D、E. (2013•衡阳)如图,已知抛物线经过A(1,0),B(0,3)两点,对称轴是x=-1.
(2013•衡阳)如图,已知抛物线经过A(1,0),B(0,3)两点,对称轴是x=-1. 如图,已知抛物线经过原点O和x轴上另一点A,它的对称轴x=2与x轴交于点C,直线y=-2x-1经过抛物线上一点B(-2,m),且与y轴、直线x=2分别交于点D、E,
如图,已知抛物线经过原点O和x轴上另一点A,它的对称轴x=2与x轴交于点C,直线y=-2x-1经过抛物线上一点B(-2,m),且与y轴、直线x=2分别交于点D、E, 如图,已知抛物线经过坐标原点,与x轴的另一个交点为A,且顶点M坐标为(1,2),
如图,已知抛物线经过坐标原点,与x轴的另一个交点为A,且顶点M坐标为(1,2),