Question

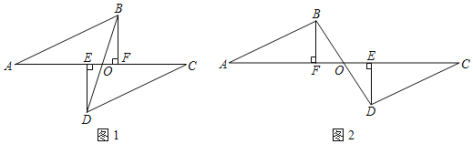
【题目】已知点A、E、F、C在一条直线上，AE＝CF，过点E、F分别作DE⊥AC，BF⊥AC，且AB＝CD.连接BD，交AC于点O.

(1)如图1，求证：BF＝DE.

(2)将△DEC沿AC方向平移到如图2的位置，其余条件不变，若BF＝3cm，请直接写出DE的长是多少？

Answer 1

【答案】(1)证明见解析；(2)DE=3cm.

【解析】

(1)首先由题意推出AF＝CE，∠BFA＝∠DEC＝90°，证得Rt△BFA≌Rt△DEC(HL)，便知BF＝DE；

(2)解法同(1).

(1)证明：∵DE⊥AC，BF⊥AC，

∴∠BFA＝∠DEC＝90°.

又∵AE＝CF，

∴AE+EF＝CF+EF，即AF＝CE，

在Rt△BFA与Rt△DEC中，

，

∴Rt△BFA≌Rt△DEC(HL)，

∴BF＝DE，

(2)解：∵DE⊥AC，BF⊥AC，

∴∠BFA＝∠DEC＝90°.

又∵AE＝CF，

∴AE﹣EF＝CF﹣EF，即AF＝CE，

在Rt△BFA与Rt△DEC中，

，

∴Rt△BFA≌Rt△DEC(HL)，

∴BF＝DE＝3cm.