��Ŀ����
����ͼ������ʾ������������ϵ��Ҳ��������������������ϵ������ͼ��������ͼ��֮��Ĺ�ϵ������˼�뷽����Ϊ���ν�ϣ����Ǹ�ѧ���ġ���������˷���ʽ���ͺܺõ���������һ˼�뷽���������������ν�ϵ�˼��������������
��ͼ��һ���߳�Ϊ1�������Σ�����ȡ�����ε�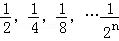 ������ͼʾ���ǿ���֪������һ��ȡ��
������ͼʾ���ǿ���֪������һ��ȡ�� ��ʣ
��ʣ ����
���� =1��
=1�� ��ǰ����ȡ��
��ǰ����ȡ�� +
+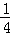 ��ʣ
��ʣ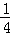 ����
���� +
+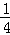 =1��
=1��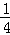 ��ǰ����ȡ��
��ǰ����ȡ��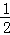 +
+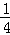 +
+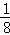 ��ʣ
��ʣ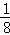 ����
����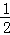 +
+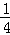 +
+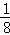 =1��
=1��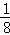 ����ǰn��ȡ�ߺ�ʣ��_________��������_________��=��_________����
����ǰn��ȡ�ߺ�ʣ��_________��������_________��=��_________����
�����������㣺
��1��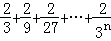 =��_________����
=��_________����
��2��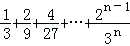 =��_________����
=��_________����
��3��2��22��23��24��25��26������22011+22012������д��������̣�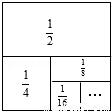
 ��
�� +
+ +
+ +��
+�� =1��
=1�� ��
��
��1��1�� ��2��1��
��2��1�� ��3��6
��3��6
��������
�����������1���������⻭��ͼ�Σ�����ȡ����������� ��
�� ��
�� ���ҳ����ɼ��ɣ�
���ҳ����ɼ��ɣ�
��2���������⻭��ͼ�Σ�����ȡ����������� ��
�� ��
�� ���ҳ����ɼ��ɣ�
���ҳ����ɼ��ɣ�
��3������ͬ�����ݵij˷����м��㼴�ɣ�
�⣺�ߵ�һ��ȡ�� ��ʣ
��ʣ ����
���� =1��
=1�� ��
��
ǰ����ȡ�� +
+ ��ʣ
��ʣ ����
���� +
+ =1��
=1�� ��
��
ǰ����ȡ�� +
+ +
+ ��ʣ
��ʣ ����
���� +
+ +
+ =1��
=1�� ��
��
��ǰn��ȡ�ߺ�ʣ ����
���� +
+ +
+ +��
+�� =1��
=1�� ��
��
�ʴ�Ϊ�� ��
�� +
+ +
+ +��
+�� =1��
=1�� ��
��
��1����ͼ��ʾ��

��ͼ��֪�� +
+ +
+ +��+
+��+ =1��
=1�� ��
��
�ʴ�Ϊ��1�� ��
��
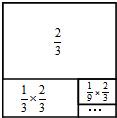
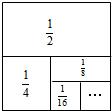
��2����ͼ��һ���߳�Ϊ1�������Σ�����ͼʾ

��ͼ��֪�� +
+ +
+ +��+
+��+ =1��
=1�� ��
��
�ʴ�Ϊ��1�� ��
��
��3��2��22��23��24��25��26������22011+22012
=2��22012��2��2010+2��2009+2��2008+��+2��1��+22012
=2��22012��1��2��2010��+22012
=2��22012+4+22012
=6��
���㣺��ʽ�Ļ������
���������⿼�������ʽ�ļӼ����������⻭��ͼ�Σ��������ν������ǽ�����Ĺؼ���

 ��У����ϵ�д�
��У����ϵ�д�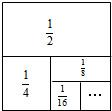

 n��ȡ�ߺ�ʣ
n��ȡ�ߺ�ʣ ��
�� ��
��
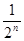 ������ͼʾ���ǿ���֪����
������ͼʾ���ǿ���֪����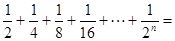 ��
��
 ��
�� ��
�� ��
��
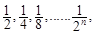 ����ͼʾ���ǿ���֪������һ��ȡ��
����ͼʾ���ǿ���֪������һ��ȡ��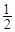 ��ʣ
��ʣ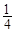 ��ʣ
��ʣ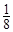 ��ʣ
��ʣ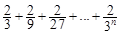 =
��
=
��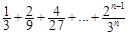 =
��
=
��