Question

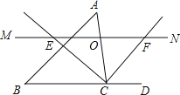
【题目】如图，点、分别在射线、上运动（不与点重合）.

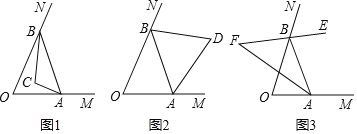
（1）如图1，若，、的平分线交于点，求的度数；

（2）如图2，若，的外角、的平分线交于点，则等于______度（用含字母的代数式表示）；

（3）如图3，若，是的平分线，的反向延长线与的平分线交于点.试问：随着点、的运动，的大小会变吗？如果不会，求的度数；如果会，请说明理由.

Answer 1

【答案】（1）；（2）；（3）的度数不变，；理由见解析.

【解析】

（1）根据三角形内角和定理得到∠OBA+∠OAB=110°，根据角平分线的定义计算即可；

（2）根据三角形内角和定理得到∠NBA+∠MAB=180°+n°，根据角平分线的定义计算即可；

（3）根据三角形的外角性质得到∠NBA﹣∠BAO=∠MON=70°，根据角平分线的定义、三角形的外角性质计算即可．

（1）∵∠MON=70°，∴∠OBA+∠OAB=180°﹣70°=110°．

∵BC、AC分别为∠OBA、∠OAB的平分线，∴∠ABC∠OBA，∠BAC∠OAB，∴∠ABC+∠BAC（∠OBA+∠OAB）=55°，∴∠ACB=180°﹣55°=125°；

（2）∵∠MON=n°，∴∠OBA+∠OAB=180°﹣n°，∴∠NBA+∠MAB=360°-（180°-n°）=180°+n°．

∵BD、AD分别为∠NBA、∠MAB的平分线，∴∠DBA∠NBA，∠DAB∠MAB，∴∠DBA+∠DAB（∠NBA+∠MAB）=90°n°，∴∠ADB=180°﹣（90°n°）=90°n°．

故答案为：90n；

（3）∠F的大小不变，理由如下：

∵BE是∠ABN的平分线，AF是∠OAB的平分线，∴∠EBA∠NBA，∠BAF∠BAO．

∵∠NBA﹣∠BAO=∠MON=70°，∴∠F=∠EBA﹣∠BAF（∠NBA﹣∠BAO）=35°．