题目内容
已知一次函数y=kx+b的图象与正比例函数y= x的图象交于点A,并且与y轴交于点B(0,-6),△AOB的面积为9,求该一次函数的解析式.
x的图象交于点A,并且与y轴交于点B(0,-6),△AOB的面积为9,求该一次函数的解析式.
解:∵一次函数与y轴交于点B(0,-6),
∴OB=6,
∵△AOB的面积为9,
∴ ×6•h=9,
×6•h=9,
解得h=3,
所以,点A的横坐标是-3或3,
当点A的横坐标是-3时,点A的纵坐标是 ×(-3)=-1,
×(-3)=-1,
点A的横坐标是3时,点A的纵坐标是 ×3=1,
×3=1,
所以,点A的坐标是(-3,-1)或(3,1),
∵一次函数经过点A、B,
∴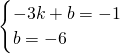 或
或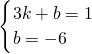 ,
,
解得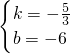 或
或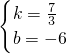 .
.
所以该一次函数的解析式为y=- x-6或y=
x-6或y= x-7.
x-7.
分析:根据三角形的面积求出点A的横坐标的长度,然后分两种情况求出点A的坐标,再利用待定系数法求一次函数解析式即可.
点评:本题考查了两直线相交的问题,待定系数法求一次函数解析式,根据三角形的面积求出点B的横坐标,从而得到点A的坐标是解题的关键.
∴OB=6,
∵△AOB的面积为9,
∴
 ×6•h=9,
×6•h=9,解得h=3,
所以,点A的横坐标是-3或3,
当点A的横坐标是-3时,点A的纵坐标是
 ×(-3)=-1,
×(-3)=-1,点A的横坐标是3时,点A的纵坐标是
 ×3=1,
×3=1,所以,点A的坐标是(-3,-1)或(3,1),
∵一次函数经过点A、B,
∴
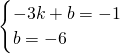 或
或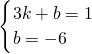 ,
,解得
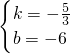 或
或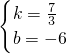 .
.所以该一次函数的解析式为y=-
 x-6或y=
x-6或y= x-7.
x-7.分析:根据三角形的面积求出点A的横坐标的长度,然后分两种情况求出点A的坐标,再利用待定系数法求一次函数解析式即可.
点评:本题考查了两直线相交的问题,待定系数法求一次函数解析式,根据三角形的面积求出点B的横坐标,从而得到点A的坐标是解题的关键.

练习册系列答案
相关题目
 已知一次函数y=kx+2的图象经过A(-1,1).
已知一次函数y=kx+2的图象经过A(-1,1). m≠0)的图象相交于点 A(1,3)、B(n,-1)两点.
m≠0)的图象相交于点 A(1,3)、B(n,-1)两点.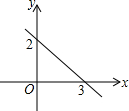 已知一次函数y=kx+b的图象如图所示,指出k、b的符号,并求出k和b的值.
已知一次函数y=kx+b的图象如图所示,指出k、b的符号,并求出k和b的值.