题目内容
1. 如图,已知⊙C与x轴交于A(1,0),B(5,0)两点,点C的纵坐标为$\sqrt{5}$,求⊙C的半径.
如图,已知⊙C与x轴交于A(1,0),B(5,0)两点,点C的纵坐标为$\sqrt{5}$,求⊙C的半径.
分析 先根据AB两点的坐标求出AB的长,作DC⊥AB于点D,根据垂径定理求出AD的长,再由勾股定理可求出AC的长即可.
解答  解:∵A(1,0),B(5,0),
解:∵A(1,0),B(5,0),
∴AB=5-1=4,
作DC⊥AB于点D,则AD=$\frac{1}{2}$AB=$\frac{1}{2}$×4=2,
在Rt△ABC中,AC=$\sqrt{C{D}^{2}+A{D}^{2}}$=$\sqrt{(\sqrt{5})^{2}+{2}^{2}}$=3.
∴⊙C的半径是3.
点评 本题考查的是垂径定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
相关题目
4.某化肥厂生产的化肥产量经过两年增长21%,则每年比上一年平均增长的百分数为( )
| A. | 10% | B. | 10.5% | C. | 11% | D. | 12% |
9.下列各式中,运算正确的是( )
| A. | 3a-2a=1 | B. | a2+a2=a4 | C. | -3ab+2ab=-ab | D. | 2x+3y=5xy |
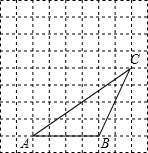 如图,△ABC的顶点都在方格纸的格点上,将△ABC向左平移1格,再向上平移3格,其中每个格子的边长为1个单位长度.
如图,△ABC的顶点都在方格纸的格点上,将△ABC向左平移1格,再向上平移3格,其中每个格子的边长为1个单位长度.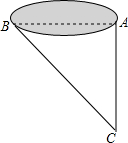 如图所示,某工程队修建高速公路,需打通一条东西走向的隧道AB,为了测得AB的长,工程队在A处正南方向800米的C处测得BC=1000米,则隧道AB的长为600米.
如图所示,某工程队修建高速公路,需打通一条东西走向的隧道AB,为了测得AB的长,工程队在A处正南方向800米的C处测得BC=1000米,则隧道AB的长为600米.
 几何证明:
几何证明: