题目内容
某电子厂商投产一种新型电子产品,每件制造成本为18元,试销过程中发现,每月销售量 (万件)与销售单价
(万件)与销售单价 (元)之间的关系可以近似地看作一次函数
(元)之间的关系可以近似地看作一次函数 .(利润=售价-制造成本)
.(利润=售价-制造成本)
(1)写出每月的利润 (万元)与销售单价
(万元)与销售单价 (元)之间的函数关系式;
(元)之间的函数关系式;
(2)当销售单价为多少元时,厂商每月获得的利润为440万元?
(3)根据相关部门规定,这种电子产品的销售单价不能高于40元,如果厂商每月的制造成本不超过540万元,那么当销售单价为多少元时,厂商每月获得的利润最大?最大利润为多少万元?
(1)z=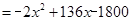 (2)440 (3)510
(2)440 (3)510
解析试题分析:解:(1)根据每月的利润z=(x-18)y,再把y=-2x+100代入即可求出z与x之间的函数解析式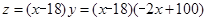 3分
3分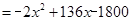 ,
,
∴z与x之间的函数解析式为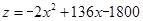 ;
;
(2)当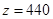 时,
时,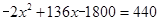
解得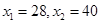
因此,当销售单价为28或40元时,厂商每月获得的利润为440万元 7分
(3)由题意,得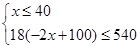
解得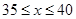 10分
10分
配方得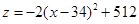
∴当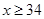 时,z随x的增大而减小
时,z随x的增大而减小
∴当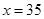 时,z最大为510万元.
时,z最大为510万元.
当销售单价为35元时,厂商每月获得的利润最大,为510万元. 12分
考点:一元二次方程与实际问题
点评:此题主要考察学生用二次函数去解决销售利润的实际问题,解答此类题,关键理解题意,找出等量关系,列出关系式,运用配方法或公式法求函数的最值。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 (万件)与销售单价
(万件)与销售单价 (元)之间的关系可以近似地看作一次函数
(元)之间的关系可以近似地看作一次函数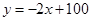 .(利润=售价-制造成本)
.(利润=售价-制造成本) (万元)与销售单价
(万元)与销售单价 (万件)与销售单价
(万件)与销售单价 (元)之间的关系可以近似地看作一次函数
(元)之间的关系可以近似地看作一次函数 .(利润=售价-制造成本)
.(利润=售价-制造成本) (万元)与销售单价
(万元)与销售单价