题目内容
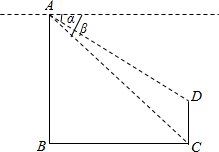如图所示，两幢建筑物的水平距离为36m，从A点测量D点的俯角α为36°，测量C点的俯角β为45°，求这两幢建筑物的高度．（精确到0.1m）分析：首先过点D作DE⊥AB于点E，可得四边形BCDE是矩形，然后在Rt△ABC中，∠ACB=β=45°，可得AB=BC=36.0（m），在Rt△AED中，∠ADE=α=36°，可得AE=DE•tan36°，继而求得答案．
解答：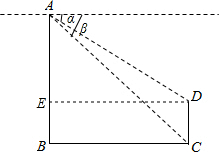
解：过点D作DE⊥AB于点E，
则四边形BCDE是矩形，
∴DE=BC=36m，BE=CD，
在Rt△ABC中，∠ACB=β=45°，
∴AB=BC=36.0（m），
在Rt△AED中，∠ADE=α=36°，
∴AE=DE•tan36°≈36×0.73≈26.3（m），
∴BE=AB-AE=9.7（m）．
答：这两幢建筑物的高度分别约为：36.0m与9.7m．
解：过点D作DE⊥AB于点E，则四边形BCDE是矩形，
∴DE=BC=36m，BE=CD，
在Rt△ABC中，∠ACB=β=45°，
∴AB=BC=36.0（m），
在Rt△AED中，∠ADE=α=36°，
∴AE=DE•tan36°≈36×0.73≈26.3（m），
∴BE=AB-AE=9.7（m）．
答：这两幢建筑物的高度分别约为：36.0m与9.7m．
点评：此题考查了俯角的定义．注意能借助俯角构造直角三角形并解直角三角形是解此题的关键．
练习册系列答案
阅读快车系列答案
相关题目
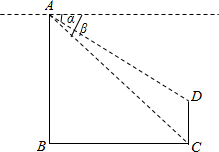如图所示，两幢建筑物的水平距离为36m，从A点测量D点的俯角α为36°，测量C点的俯角β为45°，求这两幢建筑物的高度．（精确到0.1m）