题目内容
10. 已知,如图,在平面直角坐标系xOy中,二次函数y=ax2-$\frac{7}{3}x+c$的图象经过点、A(0,8)、B(6,2)、C(9,m),延长AC交x轴于点D.
已知,如图,在平面直角坐标系xOy中,二次函数y=ax2-$\frac{7}{3}x+c$的图象经过点、A(0,8)、B(6,2)、C(9,m),延长AC交x轴于点D.(1)求这个二次函数的解析式及的m值;
(2)求∠ADO的余切值;
(3)过点B的直线分别与y轴的正半轴、x轴、线段AD交于点P(点A的上方)、M、Q,使以点P、A、Q为顶点的三角形与△MDQ相似,求此时点P的坐标.
分析 (1)把点A、B的坐标代入函数解析式求得系数a、c的值,从而得到函数解析式,然后把点C的坐标代入来求m的值;
(2)由点A、C的坐标求得直线AC的解析式,然后根据直线与坐标轴的交点的求法得到点D的坐标,所以结合锐角三角函数的定义解答即可;
(3)根据相似三角形的对应角相等进行解答.
解答 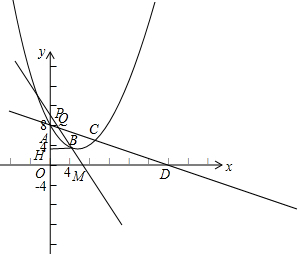 解:(1)把A(0,8)、B(6,2)代入y=ax2-$\frac{7}{3}x+c$,得
解:(1)把A(0,8)、B(6,2)代入y=ax2-$\frac{7}{3}x+c$,得
$\left\{\begin{array}{l}{8=c}\\{2=a×{6}^{2}-\frac{7}{3}×6+c}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=\frac{2}{9}}\\{c=8}\end{array}\right.$,
故该二次函数解析式为:y=$\frac{2}{9}$x2-$\frac{7}{3}$x+8.
把C(9,m),代入y=$\frac{2}{9}$x2-$\frac{7}{3}$x+8得到:m=y=$\frac{2}{9}$×92-$\frac{7}{3}$×9+8=5,即m=5.
综上所述,该二次函数解析式为y=$\frac{2}{9}$x2-$\frac{7}{3}$x+8,m的值是5;
(2)由(1)知,点C的坐标为:(9,5),
又由点A的坐标为(0,8),
所以直线AC的解析式为:y=-$\frac{1}{3}$x+8,
令y=0,则0=-$\frac{1}{3}$x+8,
解得x=24,
即OD=24,
所以cot∠ADO=$\frac{OD}{OA}$=$\frac{24}{8}$=3,即cot∠ADO=3;
(3)在△APQ与△MDQ中,∠AQP=∠MQD.
要使△APQ与△MDQ相似,则∠APQ=∠MDQ或∠APQ=∠DMQ(根据题意,这种情况不可能),
∴cot∠APQ=cot∠MDQ=3.
作BH⊥y轴于点H,
在直角△PBH中,cot∠P=$\frac{PH}{BH}$=3,
∴PH=18,OP=20,
∴点P的坐标是(0,20).
点评 本题是二次函数的综合题型,其中涉及到的知识点有待定系数法求二次函数、一次函数解析式,相似三角形的判定与性质,锐角三角函数的定义.在求有关动点问题时要注意分析题意分情况讨论结果.

 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案| A. | 28.30千克 | B. | 27.70千克 | C. | 28.51千克 | D. | 27.80千克 |
| A. | $\frac{3x}{y}$=$\frac{9}{2}$ | B. | $\frac{x+3}{y+3}$=$\frac{6}{5}$ | C. | $\frac{x-3}{y-2}$=$\frac{3}{2}$$•\frac{x}{y}$ | D. | $\frac{x+y}{x}$=$\frac{5}{2}$ |
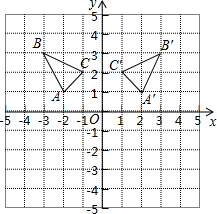 如图是一个的正方形格纸,△ABC中A点坐标为(-2,1).
如图是一个的正方形格纸,△ABC中A点坐标为(-2,1). 作图:在∠AOB内找一点P,使点到角两边距离相等,不写作法但要保留作图痕迹.
作图:在∠AOB内找一点P,使点到角两边距离相等,不写作法但要保留作图痕迹.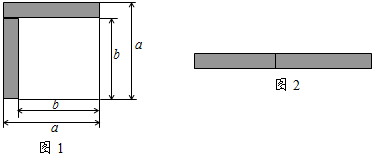
 如图,矩形ABCD中,点E是边AD的中点,BE交对角线AC于点F,则△AFE与△BCF的面积比等于$\frac{1}{4}$.
如图,矩形ABCD中,点E是边AD的中点,BE交对角线AC于点F,则△AFE与△BCF的面积比等于$\frac{1}{4}$.