题目内容
 (2011•利川市一模)小刚与小亮一起玩一种转盘游戏.图是两个完全相同的转盘,每个转盘分成面积相等的三个区域,分别用“1”、“2”、“3”表示.固定指针,同时转动两个转盘,任其自由停止.
(2011•利川市一模)小刚与小亮一起玩一种转盘游戏.图是两个完全相同的转盘,每个转盘分成面积相等的三个区域,分别用“1”、“2”、“3”表示.固定指针,同时转动两个转盘,任其自由停止.(1)求两指针指的数字之和等于4的概率;
(2)若两指针指的数字都为奇数,则小刚获胜;否则,小亮获胜.游戏公平吗?为什么?
分析:(1)首先根据题意画出树状图,然后由树状图求得所有等可能的结果与两指针指的数字之和等于4的情况,再利用概率公式求解即可求得答案;
(2)根据(1)中的树状图,即可求得小刚获胜与小亮获胜的概率,比较概率的大小,即可求得答案.
(2)根据(1)中的树状图,即可求得小刚获胜与小亮获胜的概率,比较概率的大小,即可求得答案.
解答:解:(1)画树状图得:

∵共有9种等可能的结果,两指针指的数字之和等于4的有3种情况,
∴两指针指的数字之和等于4的概率为:
=
;
(2)游戏不公平.
理由:∵两指针指的数字都为奇数的有2种情况,
∴P(小刚获胜)=
,P(小亮获胜)=
;
∴P(小刚获胜)≠P(小亮获胜),
∴游戏不公平.

∵共有9种等可能的结果,两指针指的数字之和等于4的有3种情况,
∴两指针指的数字之和等于4的概率为:
| 3 |
| 9 |
| 1 |
| 3 |
(2)游戏不公平.
理由:∵两指针指的数字都为奇数的有2种情况,
∴P(小刚获胜)=
| 2 |
| 9 |
| 7 |
| 9 |
∴P(小刚获胜)≠P(小亮获胜),
∴游戏不公平.
点评:本题考查的是游戏公平性的判断.判断游戏公平性就要计算每个事件的概率,概率相等就公平,否则就不公平.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
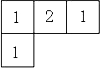 (2011•利川市一模)如图所示,是几个相同小正方体所搭成几何体的俯视图,小正方形内的数字表示在该位置的小正方体的个数.则这个几何体的主视图是( )
(2011•利川市一模)如图所示,是几个相同小正方体所搭成几何体的俯视图,小正方形内的数字表示在该位置的小正方体的个数.则这个几何体的主视图是( ) (2011•利川市一模)如图,反映的是九(3)班学生某次数学考试成绩不及格、及格、优分的人数分布直方图和扇形统计图(部分),则下列说法中不正确的是( )
(2011•利川市一模)如图,反映的是九(3)班学生某次数学考试成绩不及格、及格、优分的人数分布直方图和扇形统计图(部分),则下列说法中不正确的是( )