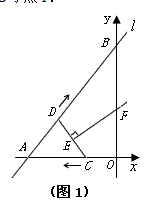题目内容
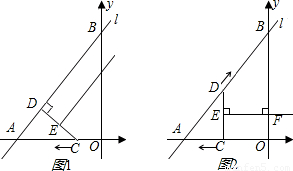
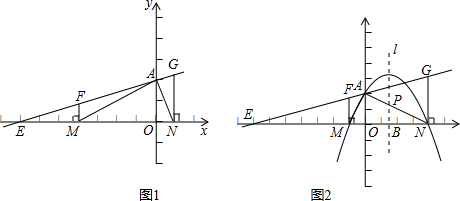
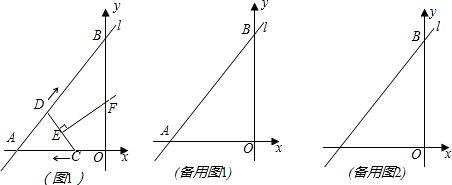
如图1,已知直线l的解析式为 ,它与x轴、y轴分别相交于A、B两点.点C从点O出发沿OA以每秒1个单位的速度向点A匀速运动;点D从点A出发沿AB以每秒1个单位长的速度向点B匀速运动,点C、D同时出发,当点C到达点A时同时停止运动.伴随着C、D的运动,EF始终保持垂直平分CD,垂足为E,且EF交折线AB-BO-AO于点F.
,它与x轴、y轴分别相交于A、B两点.点C从点O出发沿OA以每秒1个单位的速度向点A匀速运动;点D从点A出发沿AB以每秒1个单位长的速度向点B匀速运动,点C、D同时出发,当点C到达点A时同时停止运动.伴随着C、D的运动,EF始终保持垂直平分CD,垂足为E,且EF交折线AB-BO-AO于点F.(1)直接写出A、B两点的坐标;
(2)设点C、D的运动时间是t秒(t>0).
①用含t的代数式分别表示线段AD和AC的长度;
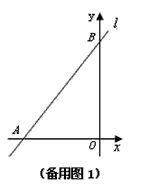
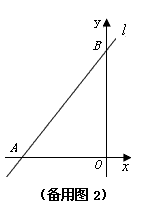
②在点F运动的过程中,四边形BDEF能否成为直角梯形?若能,求t的值;若不能,请说明理由.(可利用备用图解题)

【答案】分析:(1)已知直线的解析式,当x=0时,得出y=4,当y=0时,得出x=-3,即得出AB两点的解析式;(2)①C,D均是每秒1个单位的速度匀速运动,根据题意可简单求出;②根据实际情况分两种情况讨论当CD⊥AB时,当CD∥BO时.
解答: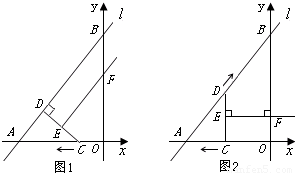 解:(1)直线的解析式为
解:(1)直线的解析式为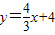 ,
,
当x=0时,得出y=4,当y=0时,得出x=-3,
所以A(-3,0),B(0,4);
(2)①因为C,D均是每秒1个单位的速度匀速运动,
所以AD=t,OC=t.
又∵A(-3,0),
∴OA=3,∴AC=3-t,
则AD=t,AC=3-t;
②能.
在Rt△ABE中,OA=3,OB=4,
根据勾股定理得: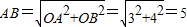 ,
,
(i)如图1,当CD⊥AB时,
∵EF⊥CD,
∴EF∥AB,
∴四边形BDEF是直角梯形,
∵∠ADC=90°,
∴∠ADC=∠A0B=90°,
又∵∠BAO=∠CAD,
∴△ADC∽△AOB,又AD=t,AC=3-t,
∴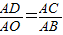 ,即
,即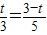 ,
,
解得 ;
;
(ii)如图2,当CD∥BO时,EF⊥BO,∴四边形BDEF是直角梯形,
此时∠ACD=90°,
∴∠ACD=∠AOB=90°,又∠DAC=∠BAO,
∴△ACD∽△AOB,又AB=t,AC=3-t,
∴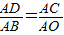 ,即
,即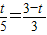 ,
,
解得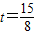 .
.
综上所得,当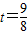 或
或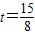 时,四边形BDEF是直角梯形.
时,四边形BDEF是直角梯形.
点评:本题考查了学生对一次函数的综合运用,难度较大,关键将知识点熟练掌握,有机结合.
解答:
 解:(1)直线的解析式为
解:(1)直线的解析式为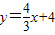 ,
,当x=0时,得出y=4,当y=0时,得出x=-3,
所以A(-3,0),B(0,4);
(2)①因为C,D均是每秒1个单位的速度匀速运动,
所以AD=t,OC=t.
又∵A(-3,0),
∴OA=3,∴AC=3-t,
则AD=t,AC=3-t;
②能.
在Rt△ABE中,OA=3,OB=4,
根据勾股定理得:
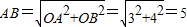 ,
,(i)如图1,当CD⊥AB时,
∵EF⊥CD,
∴EF∥AB,
∴四边形BDEF是直角梯形,
∵∠ADC=90°,
∴∠ADC=∠A0B=90°,
又∵∠BAO=∠CAD,
∴△ADC∽△AOB,又AD=t,AC=3-t,
∴
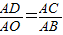 ,即
,即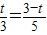 ,
,解得
 ;
;(ii)如图2,当CD∥BO时,EF⊥BO,∴四边形BDEF是直角梯形,
此时∠ACD=90°,
∴∠ACD=∠AOB=90°,又∠DAC=∠BAO,
∴△ACD∽△AOB,又AB=t,AC=3-t,
∴
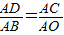 ,即
,即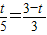 ,
,解得
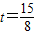 .
.综上所得,当
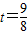 或
或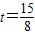 时,四边形BDEF是直角梯形.
时,四边形BDEF是直角梯形.
点评:本题考查了学生对一次函数的综合运用,难度较大,关键将知识点熟练掌握,有机结合.

练习册系列答案
相关题目
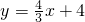 ,它与x轴、y轴分别相交于A、B两点.点C从点O出发沿OA以每秒1个单位的速度向点A匀速运动;点D从点A出发沿AB以每秒1个单位长的速度向点B匀速运动,点C、D同时出发,当点C到达点A时同时停止运动.伴随着C、D的运动,EF始终保持垂直平分CD,垂足为E,且EF交折线AB-BO-AO于点F.
,它与x轴、y轴分别相交于A、B两点.点C从点O出发沿OA以每秒1个单位的速度向点A匀速运动;点D从点A出发沿AB以每秒1个单位长的速度向点B匀速运动,点C、D同时出发,当点C到达点A时同时停止运动.伴随着C、D的运动,EF始终保持垂直平分CD,垂足为E,且EF交折线AB-BO-AO于点F.
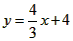 ,它与x轴、y轴分别相交于A、B两点,点C从点O出发沿OA以每秒1个单位的速度向点A匀速运动;点D从点A出发沿AB以每秒1个单位长的速度向点B匀速运动,点C、D同时出发,当点C到达点A时同时停止运动,伴随着C、D的运动,EF始终保持垂直平分CD,垂足为E,且EF交折线AB-BO-AO于点F。
,它与x轴、y轴分别相交于A、B两点,点C从点O出发沿OA以每秒1个单位的速度向点A匀速运动;点D从点A出发沿AB以每秒1个单位长的速度向点B匀速运动,点C、D同时出发,当点C到达点A时同时停止运动,伴随着C、D的运动,EF始终保持垂直平分CD,垂足为E,且EF交折线AB-BO-AO于点F。