题目内容
如果A、B、C是三个质数,而且A-B=B-C=14,那么这样的A、B、C组成的数组(A,B,C)共有
1
1
组.分析:先根据A-B=B-C=14求出A-C的值,由于A、B、C是三个质数可知A、B、C中必有一个是3的倍数,但3的倍数中只有3才是质数,把C=3代入原式即可求出A、B的对应值.
解答:解:∵A-B=B-C=14,
∴A-C=28,
∴A-B,B-C,A-C都不是3的倍数,从而A、B、C除以3的余数都不相同,
∴A、B、C中必有一个是3的倍数,但3的倍数中只有3才是质数,
∴C=3,B=17,A=31均为质数,这是唯一解,
即符合题意的数组(A,B,C)共有1组.
故答案为:1.
∴A-C=28,
∴A-B,B-C,A-C都不是3的倍数,从而A、B、C除以3的余数都不相同,
∴A、B、C中必有一个是3的倍数,但3的倍数中只有3才是质数,
∴C=3,B=17,A=31均为质数,这是唯一解,
即符合题意的数组(A,B,C)共有1组.
故答案为:1.
点评:本题考查的是质数与合数,熟知质数与合数的定义是解答此题的关键.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案
相关题目
 ,
,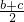 ,
, 这三个数中至少会有几个整数?请利用整数的奇偶性简单说明理由.
这三个数中至少会有几个整数?请利用整数的奇偶性简单说明理由. ,
, ,
, 这三个数中至少会有几个整数?请利用整数的奇偶性简单说明理由.
这三个数中至少会有几个整数?请利用整数的奇偶性简单说明理由. ,
, ,
, 这三个数中至少会有几个整数?请利用整数的奇偶性简单说明理由.
这三个数中至少会有几个整数?请利用整数的奇偶性简单说明理由.