Question

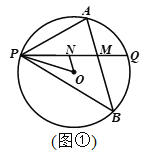
【题目】已知P是⊙O上一点，过点P作不过圆心的弦PQ，在劣弧PQ和优弧PQ上分别有动点A、B(不与P，Q重合)，连接AP、BP. 若∠APQ=∠BPQ.

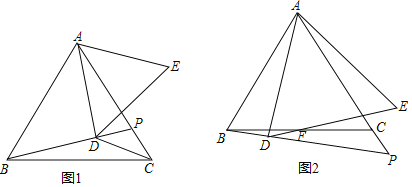
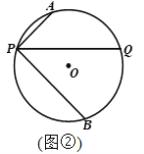
(1)如图1，当∠APQ=45°，AP=1，BP=2时，求⊙O的半径；

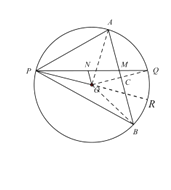
(2)如图2，选接AB，交PQ于点M，点N在线段PM上(不与P、M重合)，连接ON、OP，若∠NOP+2∠OPN=90°，探究直线AB与ON的位置关系，并证明.

Answer 1

【答案】(1) ☉O的半径是；(2)AB∥ON，证明见解析.

【解析】

(1) 连接AB，根据题意可AB为直径，再用勾股定理即可。

(2) 连接, , ,根据圆周角定理可得，从而证出

, 延长交☉0于点，则有，再根据三角形内角和定理求得=90得证.

解：(1)连接，

在☉0中，

，

是☉0的直径.

中，

☉0的半径是

(2)

证明：连接, , ,

在☉0中,

, ,

.

又,

.

在中，, ,

,即

连接，交于点

在☉0中，

延长交☉0于点，则有

,

又:，

.