题目内容
如图,Rt△AOB中,AB⊥OB,且AB = OB = 3,设直线![]() 截此三角形所得阴影部分的面积为S,则S与
截此三角形所得阴影部分的面积为S,则S与![]() 之间的函数关系的图象为下列选项中的( )
之间的函数关系的图象为下列选项中的( )


D
【解析】
试题分析:Rt△AOB中,AB⊥OB,且AB=OB=3,所以很容易求得∠AOB=∠A=45°;再由平行线的性质得出∠OCD=∠A,即∠AOD=∠OCD=45°,进而证明OD=CD=t;最后根据三角形的面积公式,解答出S与t之间的函数关系式,由函数解析式来选择图象.
:∵Rt△AOB中,AB⊥OB,且AB=OB=3,
∴∠AOB=∠A=45°,
∵CD⊥OB,
∴CD∥AB,
∴∠OCD=∠A,
∴∠AOD=∠OCD=45°,
∴OD=CD=t,
∴S△OCD=![]() ×OD×CD=
×OD×CD=![]() t2(0≤t≤3),即S=
t2(0≤t≤3),即S=![]() t2(0≤t≤3).
t2(0≤t≤3).
故S与t之间的函数关系的图象应为定义域为[0,3]、开口向上的二次函数图象;
故选D.
考点:本题主要考查的是二次函数解析式的求法及二次函数的图象特征
点评:解答本题的关键是根据三角形的面积公式,解答出S与t之间的函数关系式,由函数解析式来选择图象.

练习册系列答案
相关题目
 如图,Rt△AOB中,AB⊥OB,且AB=OB=3,设直线x=t截此三角形所得阴影部分的面积为S,则S与t之间的函数关系的图象为下列选项中的( )
如图,Rt△AOB中,AB⊥OB,且AB=OB=3,设直线x=t截此三角形所得阴影部分的面积为S,则S与t之间的函数关系的图象为下列选项中的( )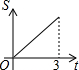


 如图在Rt△AOB中,∠BAO=90°,O为坐标原点,B在x轴正半轴上,A在第一象限.OA和AB的长是方程
如图在Rt△AOB中,∠BAO=90°,O为坐标原点,B在x轴正半轴上,A在第一象限.OA和AB的长是方程 如图,Rt△AOB中,∠AOB=90°,∠A=36°,以OB为半径作⊙O交AB于C,D为优弧BC上一点,求∠BDC的度数.
如图,Rt△AOB中,∠AOB=90°,∠A=36°,以OB为半径作⊙O交AB于C,D为优弧BC上一点,求∠BDC的度数. 如图在Rt△AOB中,∠BAO=90°,O为坐标原点,B在x轴正半轴上,A在第一象限,OA和AB的长是方程
如图在Rt△AOB中,∠BAO=90°,O为坐标原点,B在x轴正半轴上,A在第一象限,OA和AB的长是方程 如图,Rt△AOB中∠AOB=90°,点A在y=-
如图,Rt△AOB中∠AOB=90°,点A在y=-