题目内容
老师布置了下列一道题：“已知∠AOB=m°，过点O做射线OC，使得∠BOC=n°（m＞n），OE、OF分别为∠AOB和∠BOC的平分线，求∠EOF的度数？”小斌同学的答案是115°，小玲同学的答案是50°，经询问得知这两个同学的计算过程都没有出错，请你依此探究m的值为________．
165°
分析：根据角平分线的定义，求出∠EOF=∠EOB-∠FOB=
-
=50°，∠EOF=∠EOB+∠BOF=+=115°，解出方程即可求出m的值．
解答：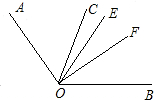
解：∵∠AOB=m°，∠BOC=n°，OE、OF分别为∠AOB和∠BOC的平分线，
∴∠BOC=2∠BOF=n°，∠AOB=2∠EOB=m°，
∴∠EOF=∠EOB-∠FOB=-=50°，
∴∠EOF=∠EOB+∠BOF=+=115°，
得出：m=165°，n=65°，
故答案为165°．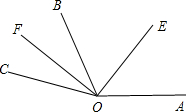
点评：本题考查了角平分线的性质，然后根据角平分线定义得出所求角与已知角的关系转化求解，难度适中．
分析：根据角平分线的定义，求出∠EOF=∠EOB-∠FOB=
-=50°，∠EOF=∠EOB+∠BOF=+=115°，解出方程即可求出m的值．解答：
解：∵∠AOB=m°，∠BOC=n°，OE、OF分别为∠AOB和∠BOC的平分线，∴∠BOC=2∠BOF=n°，∠AOB=2∠EOB=m°，
∴∠EOF=∠EOB-∠FOB=
-=50°，∴∠EOF=∠EOB+∠BOF=
+=115°，得出：m=165°，n=65°，
故答案为165°．
点评：本题考查了角平分线的性质，然后根据角平分线定义得出所求角与已知角的关系转化求解，难度适中．
练习册系列答案
相关题目