题目内容
（1）计算：2（cos30°-cos60°）+tan45°，
（2）求锐角a的值：2sin（a-30°）=1．
解：（1）原式=2×
-2×
+1
=
-1+1
=；
（2）sin（α-30°）=，
∵α为锐角，
∴α-30°=30°，
∴α=60°．
分析：（1）根据特殊角的三角函数值得到原式=2×-2×+1，然后进行乘法运算后合并即可；
（2）先变形得到sin（α-30°）=，根据sin30°=得到α-30°=30°，然后解关于α的一次方程即可．
点评：本题考查了特殊角的三角函数值：sin30°=； cos30°=；tan45°=1．
-2×+1=
-1+1=
；（2）sin（α-30°）=
，∵α为锐角，
∴α-30°=30°，
∴α=60°．
分析：（1）根据特殊角的三角函数值得到原式=2×
-2×+1，然后进行乘法运算后合并即可；（2）先变形得到sin（α-30°）=
，根据sin30°=得到α-30°=30°，然后解关于α的一次方程即可．点评：本题考查了特殊角的三角函数值：sin30°=
； cos30°=；tan45°=1． 
练习册系列答案
相关题目
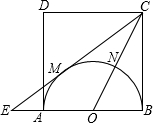半圆O于点N．
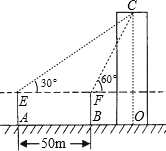如图，小平为了测量学校教学楼的高度，她先在A处利用测角仪测得楼顶C的仰角为30°，再向楼的方向直行50米到达B处，又测得楼顶C的仰角为60度．已知测角仪的高度是1.2米，请你帮助小平计算出学校教学楼的高度CO．（
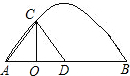的坐标（坐标轴上的一个长度单位为1m）；
