Question

等边三角形两条高线相交所成的钝角为

120

度．若不等式（b-1）x＜0的解为x＞0，则b的取值范围是

b＜1

．

Answer 1

分析：根据等边三角形性质得出∠C=60°，根据垂直定义求出∠ADC=∠BEC=90°，根据四边形的内角和定理是360度求出即可；根据不等式的两边都除以一个负数，不等式的符号要改变得出b-1＜0，求出即可．

解答：解：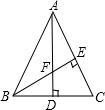
∵△ABC是等边三角形，
∴∠C=60°，
∵AD⊥BC，BE⊥AC，
∴∠ADC=∠BEC=90°，
∴∠EFD=360°-90°-90°-60°=120°；
∵不等式（b-1）x＜0的解为x＞0，
∴b-1＜0，
∴b＜1，
故答案为：120，b＜1．

点评：本题考查了等边三角形的性质和解一元一次不等式，主要考查学生的计算能力和推理能力．