题目内容
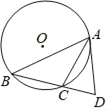
【题目】在平面直角坐标系中,二次函数![]() 的图象与
的图象与![]() 轴交于
轴交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,连接
,连接![]() 、
、![]() .
.
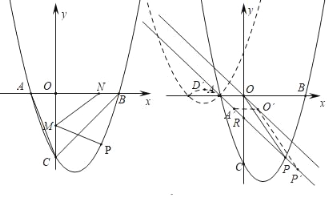
(1)点![]() 是直线
是直线![]() 下方抛物线上一点,当
下方抛物线上一点,当![]() 面积最大时,
面积最大时,![]() 为
为![]() 轴上一动点,
轴上一动点,![]() 为
为![]() 轴上一动点,记
轴上一动点,记![]() 的最小值为
的最小值为![]() ,请求出此时点
,请求出此时点![]() 的坐标及
的坐标及![]() ;
;
(2)在(1)的条件下,连接![]() 交
交![]() 轴于点
轴于点![]() ,将抛物线沿射线
,将抛物线沿射线![]() 平移,平移后的抛物线记为
平移,平移后的抛物线记为![]() ,当
,当![]() 经过点
经过点![]() 时,将抛物线
时,将抛物线![]() 位于
位于![]() 轴下方部分沿
轴下方部分沿![]() 轴翻折,翻折后所得的曲线记为
轴翻折,翻折后所得的曲线记为![]() ,点
,点![]() 为曲线
为曲线![]() 的顶点,将
的顶点,将![]() 沿直线
沿直线![]() 平移,得到
平移,得到![]() ,在平面内是否存在点
,在平面内是否存在点![]() ,使以点
,使以点![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形为菱形.若存在,请直接写出
为顶点的四边形为菱形.若存在,请直接写出![]() 的横坐标;若不存在,请说明理由.
的横坐标;若不存在,请说明理由.
【答案】(1)![]() ,
,![]() ;(2)当
;(2)当![]() 或
或![]() 时,存在点
时,存在点![]() ,使以点
,使以点![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形为菱形.
为顶点的四边形为菱形.
【解析】
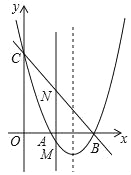
(1)如图1中,设![]() ,作PF∥y轴交BC于点F.构建二次函数求出点P坐标,如图2中,在y轴的正半轴上取一点G,连接BG,使得∠GBO=30°,作点P关于y轴的对称点H,作HF⊥BG交y轴于M,交x轴于N.由FN=
,作PF∥y轴交BC于点F.构建二次函数求出点P坐标,如图2中,在y轴的正半轴上取一点G,连接BG,使得∠GBO=30°,作点P关于y轴的对称点H,作HF⊥BG交y轴于M,交x轴于N.由FN=![]() BN,推出PM+MN+
BN,推出PM+MN+![]() BN=HM+MN+NF,根据垂线段最短可知,此时PM+MN+
BN=HM+MN+NF,根据垂线段最短可知,此时PM+MN+![]() BN的值最短,求出H,F的坐标即可解决问题.
BN的值最短,求出H,F的坐标即可解决问题.
(2)想办法求出R,D′的坐标,分两种情形分别构建方程解决问题即可.
(1)如图1中,设![]() ,作
,作![]() 轴交
轴交![]() 于点
于点![]() .
.
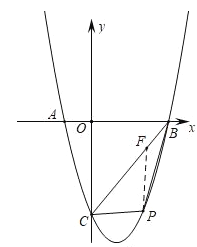
图1
由题意![]() ,
,![]() ,
,![]() ,
,
![]() 直线
直线![]() 的解析式为
的解析式为![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]()
![]() ,
,
![]() ,
,
![]() 时,
时,![]() 的面积最大,此时
的面积最大,此时![]() ,
,
如图2中,在![]() 轴的正半轴上取一点
轴的正半轴上取一点![]() ,连接
,连接![]() ,使得
,使得![]() ,作点
,作点![]() 关于
关于![]() 轴的对称点
轴的对称点![]() ,作
,作![]() 交
交![]() 轴于
轴于![]() ,交
,交![]() 轴于
轴于![]() .
.
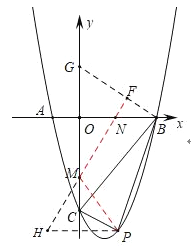
图2
![]() ,
,
![]()
![]() ,根据垂线段最短可知,此时
,根据垂线段最短可知,此时![]() 的值最短.
的值最短.
![]() 直线
直线![]() 的解析式为,
的解析式为,![]() ,
,![]() ,
,
![]() 直线
直线![]() 的解析式为
的解析式为![]() ,
,
由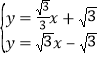 ,解得
,解得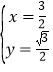 ,
,
![]() ,
,
![]() .
.
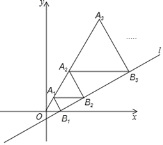
(2)如图3中,
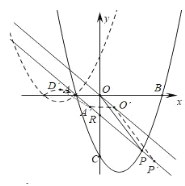
图3
由题意直线![]() 的解析式为
的解析式为![]() ,
,
![]() ,
,
![]() ,
,
![]() 直线
直线![]() 的解析式为
的解析式为![]() ,设
,设![]() ,
,
![]() 原抛物线的顶点坐标为
原抛物线的顶点坐标为![]() ,平移后抛物线经过点
,平移后抛物线经过点![]() ,此时顶点
,此时顶点![]() ,翻折后的顶点
,翻折后的顶点![]() ,
,
![]() ,
,
由题意可知当![]() 时,存在点
时,存在点![]() ,使以点
,使以点![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形为菱形,
为顶点的四边形为菱形,
![]() ,
,
解得![]() ,
,
当点![]() 在线段
在线段![]() 的垂直平分线上时,存在点
的垂直平分线上时,存在点![]() ,使以点
,使以点![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形为菱形,则有:
为顶点的四边形为菱形,则有:![]()
![]() ,
,
![]() .
.
综上所述,当![]() 或
或![]() 时,存在点
时,存在点![]() ,使以点
,使以点![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形为菱形.
为顶点的四边形为菱形.