Question

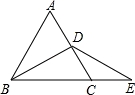
如图，△ABC中，∠A=36°，AB=AC，BD平分∠ABC，DE∥BC，则图中等腰三角形的个数(     )

A．1个  B．3个   C．4个  D．5个

Answer 1

D【考点】等腰三角形的判定与性质；角平分线的性质．

【分析】首先根据已知条件分别计算图中每一个三角形每个角的度数，然后根据等腰三角形的判定：等角对等边解答，做题时要注意，从最明显的找起，由易到难，不重不漏．

【解答】解：∵AB=AC，∠A=36°∴△ABC是等腰三角形，

∠ABC=∠ACB==72°，

BD平分∠ABC，∴∠EBD=∠DBC=36°，

∵ED∥BC，

∴∠AED=∠ADE=72°，∠EDB=∠CBC=36°，

∴在△ADE中，∠AED=∠ADE=72°，AD=AE，△ADE为等腰三角形，

在△ABD中，∠A=∠ABD=36°，AD=BD，△ABD是等腰三角形，

在△BED中，∠EBD=∠EDB=36°，ED=BE，△BED是等腰三角形，

在△BDC中，∠C=∠BDC=72°，BD=BC，△BDC是等腰三角形，

所以共有5个等腰三角形．

故选D．

【点评】本题考查了等腰三角形的性质及等腰三角形的判定，角的平分线的性质，两直线平行的性质；求得各个角的度数是正确解答本题的关键．