题目内容
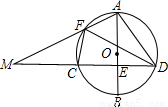
(2004•三明)如图①是一张眼镜的照片,两镜片下半部分轮廓可以近似看成抛物线形状.建立如图②直角坐标系,已知左轮廓线端点A、B间的距离为4cm,点A、B与右轮廓线端点D、E均在平行于x轴的直线上,最低点C在x轴上,且与AB的距离CH=1cm,y轴平分BD,BD=2cm.解答下列问题:(1)求轮廓线ACB的函数解析式;(写出自变量x的取值范围)
(2)由(1)写出右轮廓线DFE对应的函数解析式及自变量x的取值范围.
【答案】分析:(1)易得A、B、C三点的坐标,根据待定系数法就可以求出抛物线的解析式;
(2)轮廓线DFE是抛物线.F是顶点,并且经过点D、E,根据待定系数法就可求出抛物线的解析式.
解答:解:(1)设左轮廓线ACB的抛物线解析式为y=ax2+bx+c(a≠0)(1分)
∵A(-5,1),B(-1,1),C(-3,0)
∴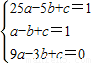
解得: ;
;
∴左轮廓线ACB的抛物线解析式为:y= x2+
x2+ x+
x+ (-5≤x≤-1)(9分);
(-5≤x≤-1)(9分);
(2)由左右两轮廓线关于y轴对称,
又y= (x+3)2,顶点C(-3,0),
(x+3)2,顶点C(-3,0),
∴顶点C关于y轴对称点F(3,0)且a1= ,
,
∴右轮廓线DFE对应的函数解析式为y= (x-3)2,即:y=
(x-3)2,即:y= x2-
x2- x+
x+ (1≤x≤5).(12分)
(1≤x≤5).(12分)
点评:本题主要考查了待定系数法求抛物线的解析式,难易程度适中.
(2)轮廓线DFE是抛物线.F是顶点,并且经过点D、E,根据待定系数法就可求出抛物线的解析式.
解答:解:(1)设左轮廓线ACB的抛物线解析式为y=ax2+bx+c(a≠0)(1分)
∵A(-5,1),B(-1,1),C(-3,0)
∴
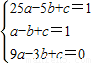
解得:
 ;
;∴左轮廓线ACB的抛物线解析式为:y=
 x2+
x2+ x+
x+ (-5≤x≤-1)(9分);
(-5≤x≤-1)(9分);(2)由左右两轮廓线关于y轴对称,
又y=
 (x+3)2,顶点C(-3,0),
(x+3)2,顶点C(-3,0),∴顶点C关于y轴对称点F(3,0)且a1=
 ,
,∴右轮廓线DFE对应的函数解析式为y=
 (x-3)2,即:y=
(x-3)2,即:y= x2-
x2- x+
x+ (1≤x≤5).(12分)
(1≤x≤5).(12分)点评:本题主要考查了待定系数法求抛物线的解析式,难易程度适中.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目