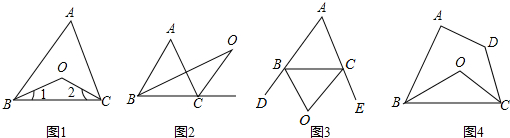
题目内容
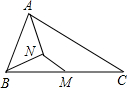 在△ABC中,M是BC中点,AN平分∠BAC,AN⊥BN于N,AB,AC,MN之间的数量关系为________.
在△ABC中,M是BC中点,AN平分∠BAC,AN⊥BN于N,AB,AC,MN之间的数量关系为________.
MN= (AC-AB)
(AC-AB)
分析:首先证明△ABN≌△AEN,可得AE=AB,BN=NE,再由条件M是BC中点,可知MN是△BEC的中位线,可得MN= EC,再有EC=AC-AE,AE=AB,可得MN=
EC,再有EC=AC-AE,AE=AB,可得MN= (AC-AB).
(AC-AB).
解答: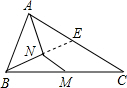 解:延长线段BN交AC于E.
解:延长线段BN交AC于E.
∵AN平分∠BAC,
∴∠BAN=∠EAN,
∵AN⊥BN,
∴∠ANE=∠ANB=90°,
在△ANB和△ANE中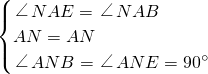 ,
,
∴△ABN≌△AEN(ASA),
∴AE=AB,BN=NE,
又∵M是△ABC的边BC的中点,
∴MN= CE,
CE,
∴MN= (AC-AE)=
(AC-AE)= (AC-AB),
(AC-AB),
故答案为:MN= (AC-AB).
(AC-AB).
点评:此题主要考查了三角形中位线定理,全等三角形的判定,关键是证出△ABN≌△AEN,得到AE=AB,BN=NE,熟记三角形中位线定理:三角形的中位线平行于第三边,并且等于第三边的一半.
 (AC-AB)
(AC-AB)分析:首先证明△ABN≌△AEN,可得AE=AB,BN=NE,再由条件M是BC中点,可知MN是△BEC的中位线,可得MN=
 EC,再有EC=AC-AE,AE=AB,可得MN=
EC,再有EC=AC-AE,AE=AB,可得MN= (AC-AB).
(AC-AB).解答:
 解:延长线段BN交AC于E.
解:延长线段BN交AC于E.∵AN平分∠BAC,
∴∠BAN=∠EAN,
∵AN⊥BN,
∴∠ANE=∠ANB=90°,
在△ANB和△ANE中
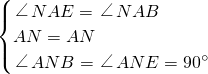 ,
,∴△ABN≌△AEN(ASA),
∴AE=AB,BN=NE,
又∵M是△ABC的边BC的中点,
∴MN=
 CE,
CE,∴MN=
 (AC-AE)=
(AC-AE)= (AC-AB),
(AC-AB),故答案为:MN=
 (AC-AB).
(AC-AB).点评:此题主要考查了三角形中位线定理,全等三角形的判定,关键是证出△ABN≌△AEN,得到AE=AB,BN=NE,熟记三角形中位线定理:三角形的中位线平行于第三边,并且等于第三边的一半.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
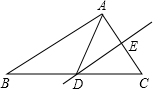 如图所示,在△ABC中,DE是AC的中垂线,AE=3cm,△ABD得周长为13cm,则△ABC的周长是
如图所示,在△ABC中,DE是AC的中垂线,AE=3cm,△ABD得周长为13cm,则△ABC的周长是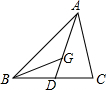 如图,在△ABC中,AD是中线,G是重心,
如图,在△ABC中,AD是中线,G是重心, 如图在△ABC中,AD是BC边上的高,BE平分∠ABD,交AD于E.已知∠BED=60°,∠BAC=50°,则∠C=( )
如图在△ABC中,AD是BC边上的高,BE平分∠ABD,交AD于E.已知∠BED=60°,∠BAC=50°,则∠C=( )