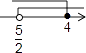题目内容
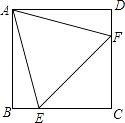
【题目】如图,△ABC是等腰直角三角形,AC=BC=a,以斜边AB上的点O为圆心的圆分别与AC,BC相切于点E,F,与AB分别交于点G,H,且EH的延长线和CB的延长线交于点D,则CD的长为 . 
【答案】![]()
a
【解析】解:如图,连接OE、OF,
∵由切线的性质可得OE=OF=⊙O的半径,∠OEC=∠OFC=∠C=90°,
∴OECF是正方形,
∵由△ABC的面积可知 ![]() ×AC×BC=
×AC×BC= ![]() ×AC×OE+
×AC×OE+ ![]() ×BC×OF,
×BC×OF,
∴OE=OF= ![]() a=EC=CF,BF=BC﹣CF=0.5a,GH=2OE=a,
a=EC=CF,BF=BC﹣CF=0.5a,GH=2OE=a,
∵由切割线定理可得BF2=BHBG,
∴ ![]() a2=BH(BH+a),
a2=BH(BH+a),
∴BH= ![]() a或BH=
a或BH= ![]() a(舍去),
a(舍去),
∵OE∥DB,OE=OH,
∴△OEH∽△BDH,
∴ ![]() =
= ![]() ,
,
∴BH=BD,CD=BC+BD=a+ ![]() a=
a= ![]() a.
a.
故答案为: ![]() a.
a.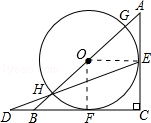
连接OE、OF,由切线的性质结合结合直角三角形可得到正方形OECF,并且可求出⊙O的半径为0.5a,则BF=a﹣0.5a=0.5a,再由切割线定理可得BF2=BHBG,利用方程即可求出BH,然后又因OE∥DB,OE=OH,利用相似三角形的性质即可求出BH=BD,最终由CD=BC+BD,即可求出答案.

 科学实验活动册系列答案
科学实验活动册系列答案【题目】某校在一次广播操比赛中,初二 (1)班、初二(2)班、初二(3)班的各项得分如下:
服装统一 | 动作整齐 | 动作准确 | |
初二(1)班 |
|
|
|
初二(2)班 |
|
|
|
初二(3)班 |
|
|
|
(1)填空:根据表中提供的信息,在服装统一方面,三个班得分的平均数是________;在动作整齐方面三个班得分的众数是________;在动作准确方面最有优势的是________班.
(2)如果服装统一、动作整齐、动作准确三个方面的重要性之比为![]() ,那么这三个班的排名顺序怎样?为什么?
,那么这三个班的排名顺序怎样?为什么?
(3)在(2)的条件下,你对三个班级中排名最靠后的班级有何建议?