Question

【题目】已知锐角△ABC中，边BC长为12，高AD长为8

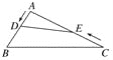
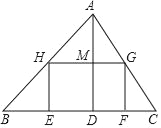
（1）如图，矩形EFGH的边GH在BC边上，其余两个顶点E、F分别在AB、AC边上，EF交AD于点K

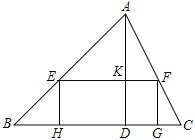
①求的值

②设EH=x，矩形EFGH的面积为S，求S与x的函数关系式，并求S的最大值

（2）若ABAC，正方形PQMN的两个顶点在△ABC一边上，另两个顶点分别在△ABC的另两边上，直接写出正方形PQMN的边长．

Answer 1

【答案】；S=－+12x，最大值为24；或．

【解析】

试题根据EF∥BC得出△AEF∽△ABC，从而得到，求出答案；根据题意得出和，将两式相加得到，根据EH=x，得出EF=12－x，根据S=EH·EF得出函数关系式，求出最大值；根据三角形相似，然后分两种情况得出答案．

试题解析：（1）①、∵EF∥BC ∴△AEF∽△ABC ∵AD⊥BC ∴AK⊥EF

∴=．

②∵①② ①+②得：

又∵EH=x，AD=8，BC=12 ∴EF=12－x

∴S=EH·EF=－+12x=－ +24 ∴S的最大值为24

（2）或．