Question

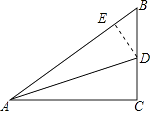
【题目】如图所示，在Rt△ACB中，∠C=90°，AC=3，BC=2，AD为中线．
（1）比较∠BAD和∠DAC的大小．
（2）求sin∠BAD．

Answer 1

【答案】
（1）解：过点D做AB的垂线，垂足记为E，

则sin∠DAE= ，sin∠DAC= ，

∵BC=2，AD为中线，

∴BD=CD=1，

∵BD＞DE，

∴CD＞DE，

∴sin∠DAE＜sin∠DAC，

∴∠BAD＜∠DAC

（2）解：∵在Rt△ACB中，∠C=90°，AC=3，BC=2，AD为中线，

∴BD=CD=1，AB= ，

∴ ，AD= ，

解得，DE= ，

∴sin∠BAD= = ．

【解析】（1）要比较∠BAD和∠DAC的大小，只要比较它们的正弦值的大小即可，根据题目中的数据可以求得它们的正弦值，从而可以解答本题；（2）根据题目中的数据可以求得DE和AD的长，从而可以求得sin∠BAD．
【考点精析】解答此题的关键在于理解解直角三角形的相关知识，掌握解直角三角形的依据：①边的关系a2+b2=c2；②角的关系：A+B=90°；③边角关系：三角函数的定义．(注意：尽量避免使用中间数据和除法)．