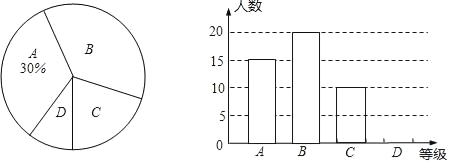
��Ŀ����
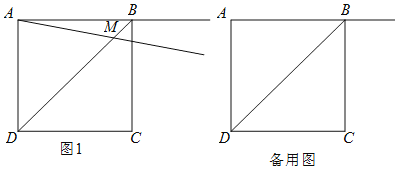
����Ŀ��������ABCD�ı߳�Ϊ2��������AB�Ƶ�A˳ʱ����ת���������������߶�BD���ڵ�M����CE��AM�ڵ�E����N���M����ֱ��CE�Գƣ�����CN��
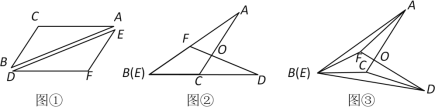
��1����ͼ����0�㣼����45��ʱ��
�������ⲹȫͼ��
���õ�ʽ��ʾ��NCE���BAM֮���������ϵ��___________��
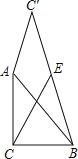
��2����45�㣼����90��ʱ��̽����NCE���BAM֮���������ϵ������֤����
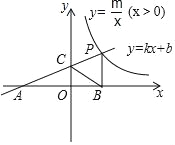
��3����0�㣼����90��ʱ������AD���е�ΪF��ֱ��д���߶�EF�������ֵ��
���𰸡���1���ٲ�ͼ���������ڡ�NCE��2��BAM����2��![]() ��NCE+��BAM��90����֤������������3��1+
��NCE+��BAM��90����֤������������3��1+![]() ��
��
��������
��1����CE��AM�ڵ�E����N���M����ֱ��CE�Գ�������CN���ɡ�ABM�ա�CBM���ɵá�BAM����BCM���ɡ�ABC����CEA��90�㣬BC��AE����һ�����ɵá�BAM����BCE�����ɵõ���MCE��2��BAM���ɵ�N���M����ֱ��CE�Գ����ɵ�CN��CM�����ɵõ���NCE����MCE�������ó���NCE��2��BAM��
��2������CM���ж���ADM�ա�CDM�����ɵõ���DAM����DCM���ٸ��ݡ�DAQ����ECQ�����ɵõ���NCE����MCE��2��DAQ����![]() ���ٸ��ݡ�BAM����BCM����BCM+��DCM��90�㣬���ɵõ�
���ٸ��ݡ�BAM����BCM����BCM+��DCM��90�㣬���ɵõ�![]() ��
��
��3�����ݡ�CEA��90�㣬���ɵõ���E����ACΪֱ����Բ������EF����Բ��Oʱ�����ɵó��߶�EF�������ֵ��
��1������ȫ��ͼ����ͼ��ʾ��
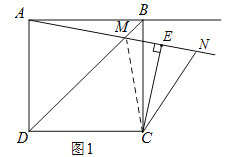
����NCE��2��BAM������������
��ͼ1������MC��
��ABCD������������AB=BC����ABM=��CBM��
��BM=BM�����ABM�ա�CBM�����BAM����BCM��
�ߡ�ABC����CEA��90�㣬BC��AE����һ�������BAM����BCE�����MCE��2��BAM��
����N���M����ֱ��CE�Գ�����CN��CM�����NCE����MCE�����NCE��2��BAM��
�ʴ�Ϊ����NCE��2��BAM��
��2��![]() ������������
������������
��ͼ������CM��
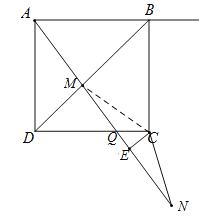
��AD��CD����ADM����CDM��DM��DM�����ADM�ա�CDM�����DAM����DCM��
�ߡ�ADQ����CEQ��90�㣬��AQD����CQE�����DAQ����ECQ�����NCE����MCE��2��DAQ����![]() ��
��
�ߡ�BAM����BCM����BCM+��DCM��90�㣬��![]() ��
��
��3����ͼ������CEA��90�㣬���E����ACΪֱ����Բ����OΪԲ��������ɵ���OF![]() CD��1��OE��OC
CD��1��OE��OC![]() AC
AC![]() ��
��
��OE+OF��EF���൱EF����Բ��Oʱ��![]() ��
��