题目内容
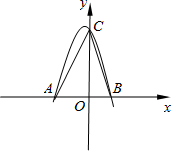如图所示，抛物线y=-x2-2x+8与x轴交于A、B两点，与y轴交于点C．则图中△ABC的面积为________．
24
分析：先令y=0求出x的值即可得出A、B两点的坐标，再令x=0求出y的值即可得出C点坐标，再根据三角形的面积公式求解即可．
解答：∵令y=0，则x1=2，x2=-4，
∴A（-4，0），B（2，0），
∵令x=0，则y=8，
∴C（0，8），
∴S△ABC=
AB•OC=×（2+4）×8=24．
故答案为：24．
点评：本题考查的是抛物线与x轴的交点，熟知坐标轴上点的坐标特点是解答此题的关键．
分析：先令y=0求出x的值即可得出A、B两点的坐标，再令x=0求出y的值即可得出C点坐标，再根据三角形的面积公式求解即可．
解答：∵令y=0，则x1=2，x2=-4，
∴A（-4，0），B（2，0），
∵令x=0，则y=8，
∴C（0，8），
∴S△ABC=
AB•OC=×（2+4）×8=24．故答案为：24．
点评：本题考查的是抛物线与x轴的交点，熟知坐标轴上点的坐标特点是解答此题的关键．
练习册系列答案
相关题目
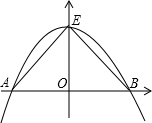如图所示，抛物线y=ax2+bx+c与两坐标轴的交点分别是A、B、E，且△ABE是等腰直角三角形，AE=BE，则下列关系式中不能成立的是（ ）| A、b=0 | B、S△ABE=c2 | C、ac=-1 | D、a+c=0 |
（2012•河源二模）已知：如图所示，抛物线y=-x2+bx+c与x轴的两个交点分别为A（1，0），B（3，0）．
（2012•槐荫区一模）如图所示，抛物线y=x2+bx+c经过A、B两点，A、B两点的坐标分别为（-1，0）、（0，-3）．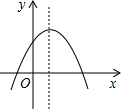
（1997•陕西）如图所示，抛物线对应的函数解析表达式只可能是（ ）
（1997•陕西）如图所示的抛物线是把y=-x2经过平移而得到的．这时抛物线过原点O和x轴正向上一点A，顶点为P；