Question

【题目】在中,BD,CE分别是,平分线,BD,CE相交于点P．

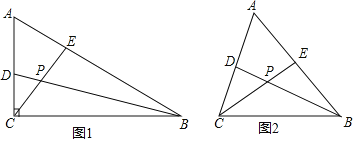
如图1,如果,则______；

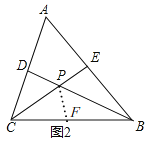
如图2,如果,不是直角,请问在中所得的结论是否仍然成立？若成立,请证明：若不成立,请说明理由．

小月同学在完成之后,发现CD、BE、BC三者之间存在着一定的数量关系,于是她在边CB上截取了,连接PF,可证≌,请你写出小月同学发现,并完成她的说理过程．

Answer 1

【答案】（1）；（2）成立，见解析；（3），见解析.

【解析】

（1）先根据三角形内角和定理求出∠ABC=90°，再利用角平分线的定义求出∠PCB=45°，∠PBC=15°，最后用三角形的内角和定理即可得出结论；

（2）先根据角平分线的意义，求出∠ACB=2∠PCB，∠ABC=2∠PBC，再根据三角形的内角和定理求出∠ABC+∠ACB=120°，最后用三角形内角和定理即可得出结论；

（3）先判断出，得出CD=CF，∠DPC=FPC=60°，进而判断出∠PBF=∠PBE，即可判断出，最后用等量代换即可得出结论.

解：（1）∵∠A=60°，∠ACB=90°,根据三角形内角和定理得,

∠ABC=180°-60°-90°=30°

,CE分别是,平分线,

∴∠PCB=∠ACB=45°，∠PBC=∠ABC=15°

在中,根据三角形的内角和定理得,

∠BPC=180°-∠PCB-∠PBC=180°-45°-15°=120°

故答案为120°；

（2）结论仍然成立,

理由：,CE分别是,平分线,

,,

∵∠A=60°

在中, ∠A+∠ABC+∠ACB=180° ,

∴∠ABC+∠ACB=180°-∠A=120°

∴2∠PCB+2∠PBC=120°,

∴∠PCB+∠PBC=60°

在中, ∠BPC+∠PCB+∠PBC=180°

∴∠BPC=180°-（∠PCB+∠PBC）=180°-60°=120°,

（3）,理由：如图2,

由知, ∠BPC=120°,

∴DPC=∴EPB=60°,在边CB上截取了,连接PF,

是的平分线,

,

在和中,,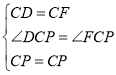

≌,

,∠DPC=∠FPC=60°,

∴∠FPB=∠BPC-∠FPC=60°=∠EPB,

是的平分线,

,

在和中,,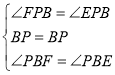

≌,,

．