题目内容

检验方程组的解时，必须将求得的未知数的值代入方程组中的每一个方程．
例1：解方程组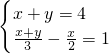数学公式
思路分析：本例这两个方程中①较简单，且x、y的系数均为1，故可把①变形，把x用y表示，或把y用x来表示皆可，然后将其代入②，消去一个未知数，化成一元一次方程，进而再求出方程组的解．
解：把①变形为y=4-x　③
把③代入②得：数学公式-数学公式=1
即数学公式-数学公式=1，数学公式=数学公式-1，数学公式=数学公式
∴x=数学公式
把x=数学公式代入③得y=4-数学公式=3数学公式
所以原方程的解是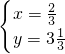数学公式．
若想知道解的是否正确，可作如下检验：
检验：把x=数学公式，y=3数学公式代入①得，左边=x+y=数学公式+3数学公式=4，右边=4．
所以左边=右边．
再把x=数学公式，y=3数学公式代入②得
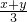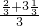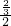左边数学公式-数学公式=数学公式-数学公式=数学公式-数学公式=1，右边=1．
所以左边=右边．
所以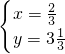数学公式是原方程组的解．

解：检验方程组的解时，必须将求得的未知数的值代入方程组中的每一个方程．
分析：题目体现了解方程组和验根的过程，要根据系数特点选择合适的方法解方程，检验时要将未知数的值代入方程组中的每一个方程．
点评：解答此题要明确，只有方程组中每个方程左、右两边的值相等了，它才是各个方程的解，即它们的公共解，从而是原方程组的解．
练习册系列答案
相关题目
　　当x=1，y=是方程组的解时，则a=________，b=________．

 

（1）若方程组①数学公式的解为数学公式，求方程组②数学公式的解时，令方程组②中的x+2=a，y-1=b，则方程组②就转化为方程组①，所以可得x+2=8.3，y-1=1.2，故方程组②的解为________．
（2）已知关于x，y的二元一次方程组③数学公式的解是数学公式，求关于x，y的二元一次方程组．

下表是按一定规律排列的一组方程组．


方程组1方程组2方程组3方程组…方程组n
方程组数学公式数学公式数学公式…数学公式
方程组的解数学公式数学公式数学公式…数学公式

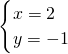（1）将方程组1的解直接填入表格中；
（2）若方程组数学公式的解是数学公式，则 a=______，b=______；该方程组是（1）中所给的方程组中的第______个；
（3）请依据方程组和它的解的变化规律，将方程组n和它的解直接填入表格中；
（4）若方程组数学公式的解是数学公式，求m的值，并判断该方程组是否符合（3）中规律．
检验方程组的解时，必须将求得的未知数的值代入方程组中的每一个方程．
例1：解方程组
x+y=4
x+y
3
-
x
2
=1

思路分析：本例这两个方程中①较简单，且x、y的系数均为1，故可把①变形，把x用y表示，或把y用x来表示皆可，然后将其代入②，消去一个未知数，化成一元一次方程，进而再求出方程组的解．
把①变形为y=4-x  ③
把③代入②得：
x+4-x
3
-
x
2
=1
即
4
3
-
x
2
=1，
x
2
=
4
3
-1，
x
2
=
1
3

∴x=
2
3

把x=
2
3
代入③得y=4-
2
3
=3
1
3

所以原方程的解是
x=
2
3
y=3
1
3
．
若想知道解的是否正确，可作如下检验：
检验：把x=
2
3
，y=3
1
3
代入①得，左边=x+y=
2
3
+3
1
3
=4，右边=4．
所以左边=右边．
再把x=
2
3
，y=3
1
3
代入②得
左边
x+y
3
-
x
2
=
2
3
+3
1
3
3
-
2
3
2
=
4
3
-
1
3
=1，右边=1．
所以左边=右边．
所以
x=
2
3
y=3
1
3
是原方程组的解．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网