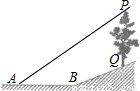
题目内容
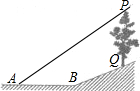 已知:如图,在坡度为i=1:2.4的斜坡BQ上有一棵香樟树PQ,柳明在A处测得树顶点P的仰角为α,并且测得水平的AB=8米,另外BQ=13米,tanα=0.75.点A、B、P、Q在同一平面上,PQ⊥AB.求:香樟树PQ的高度.
已知:如图,在坡度为i=1:2.4的斜坡BQ上有一棵香樟树PQ,柳明在A处测得树顶点P的仰角为α,并且测得水平的AB=8米,另外BQ=13米,tanα=0.75.点A、B、P、Q在同一平面上,PQ⊥AB.求:香樟树PQ的高度.
解:延长PQ交直线AB于点H. 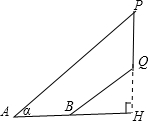
∵在Rt△QBH中,QH:BH=1:2.4.
∴设QH=x,BH=2.4x,
∵BQ=13米,
∴x2+(2.4x)2=132.
∴x=5.
∴QH=5(米),BH=12(米).
∵AB=8(米),
∴AH=20(米).
∵tanα=0.75,
∴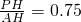 .
.
即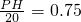 ,
,
∴PH=15(米).
∴PQ=PH-QH=15-5=10(米).
分析:先延长PQ交直线AB于点H,得直角三角形QBH,根据坡度为i=1:2.4和勾股定理求出QH和BH,从而得出AH,再由直角三角形和tanα=0.75求出PH,继而求出香樟树PQ的高度.
点评:此题考查的知识点是解直角三角形的应用,关键是构造两直角三角形根据勾股定理和三角函数求解.

∵在Rt△QBH中,QH:BH=1:2.4.
∴设QH=x,BH=2.4x,
∵BQ=13米,
∴x2+(2.4x)2=132.
∴x=5.
∴QH=5(米),BH=12(米).
∵AB=8(米),
∴AH=20(米).
∵tanα=0.75,
∴
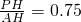 .
.即
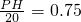 ,
,∴PH=15(米).
∴PQ=PH-QH=15-5=10(米).
分析:先延长PQ交直线AB于点H,得直角三角形QBH,根据坡度为i=1:2.4和勾股定理求出QH和BH,从而得出AH,再由直角三角形和tanα=0.75求出PH,继而求出香樟树PQ的高度.
点评:此题考查的知识点是解直角三角形的应用,关键是构造两直角三角形根据勾股定理和三角函数求解.

练习册系列答案
相关题目
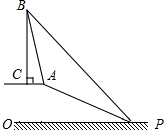
 (2013•金华模拟)已知:如图,在坡度为i=1:2.4的斜坡BQ上有一棵香樟树PQ,柳明在A处测得树顶点P的仰角为α,并且测得水平的AB=8米,另外BQ=13米,tanα=0.75.点A、B、P、Q在同一平面上,PQ⊥AB.求:香樟树PQ的高度.
(2013•金华模拟)已知:如图,在坡度为i=1:2.4的斜坡BQ上有一棵香樟树PQ,柳明在A处测得树顶点P的仰角为α,并且测得水平的AB=8米,另外BQ=13米,tanα=0.75.点A、B、P、Q在同一平面上,PQ⊥AB.求:香樟树PQ的高度.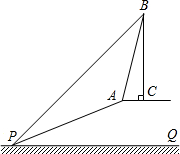 (2013•瑶海区一模)已知:如图,在大蜀山山顶有一斜坡AP的坡度为1:2.4,坡长AP为26米,在坡顶A处的同一水平面上有一座安徽卫视发射塔BC,在斜坡底P处测得该塔的塔顶B的仰角为45°,在坡顶A处测得该塔的塔顶B的仰角为76°,求:
(2013•瑶海区一模)已知:如图,在大蜀山山顶有一斜坡AP的坡度为1:2.4,坡长AP为26米,在坡顶A处的同一水平面上有一座安徽卫视发射塔BC,在斜坡底P处测得该塔的塔顶B的仰角为45°,在坡顶A处测得该塔的塔顶B的仰角为76°,求: