题目内容

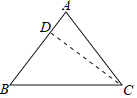
【题目】如图，在四边形ABCD中，AB∥CD．BC∥AD．

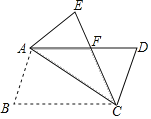
（1）求证：△ABC≌△CDA；

（2）△ABC关于对角线AC的对称图形为△AEC，EC、AD交于点F，判断△ACF的形状并说明理由．

【答案】（1）见解析；（2）△ACF是等腰三角形，见解析.

【解析】

（1）利用平行线的性质，根据ASA即可判断；

（2）只要证明∠ACF＝∠CAF，即可判断．

（1）证明：∵AB∥CD

∴∠BAC＝∠ACD，

∵BC∥AD，

∴∠ACB＝∠CAD，

∵AC＝CA，

∴△ABC≌△CDA（ASA），

（2）∵△ABC与△AEC关于AC对称，

∴∠ACB＝∠ACE，

∵AD∥BC，

∠ACB＝∠CAD，

∴∠ACF＝∠CAF，

∴FA＝FC，

∴△ACF是等腰三角形．

练习册系列答案
相关题目

【题目】已知关于x的一元二次方程x2+（2m+1）x+m2﹣2=0．

（1）若该方程有两个实数根，求m的最小整数值；

（2）若方程的两个实数根为x1，x2，且（x1﹣x2）2+m2=21，求m的值．

【题目】如图所示，在平面直角坐标系中，A（﹣1，5），B（﹣1，0），C（﹣4，3）．

（1）求出△ABC的面积；

（2）在图形中作出△ABC关于x轴的对称图形△A1B1C1，写出点A1，B1，C1的坐标；

（3）点P在y轴上，使PB+PC的长最小，请在y轴上标出点P的位置．

【题目】如图，点A、B分别在x轴的负半轴和y轴的正半轴上，点C（2，﹣2），CA、CB分别交坐标轴于D、E，CA⊥AB，且CA＝AB

（1）求点B的坐标；

（2）如图2，连接DE，求证：BD﹣AE＝DE；

（3）如图3，若点F为（4，0），点P在第一象限内，连接PF，过P作PM⊥PF交y轴于点M，在PM上截取PN＝PF，连接PO、BN，过P作∠OPG＝45°交BN于点G，求证：点G是BN的中点．

【题目】《几何原本》是一部集前人思想和欧几里得个人创造性于一体的不朽之作，它建立了一套从公理、定义出发，论证命题得到定理的几何学论证方法，形成了一个严密的逻辑体系﹣﹣﹣几何学．以下是《几何原本》第一卷中的命题6，请完成它的证明过程．

命题6：如果一个三角形有两个角相等，那么这两个角所对的边也相等．

已知：　 　．

求证：　 　．

证明：若AB≠AC，其中必有一个较大，不妨设AB＞AC，在AB上截取BD＝AC，

连接DC．

∵　 　，

　 　，

　 　，

∴△ACB≌△DBC　 　

∴∠BDC＝∠CAB　 　．

又∠BDC＞∠CAB　 　．

∴∠BDC与∠CAB即等于又大于，显然是矛盾的．

∴假设不成立，即AB＝AC．

【题目】如图，有一块含30°角的直角三角板OAB的直角边BO的长恰与另一块等腰直角三角板ODC的斜边OC的长相等，把这两块三角板放置在平面直角坐标系中，且OB＝3.

(1)若某反比例函数的图象的一个分支恰好经过点A，求这个反比例函数的解析式；

(2)若把含30°角的直角三角板绕点O按顺时针方向旋转后，斜边OA恰好落在x轴上，点A落在点A′处，试求图中阴影部分的面积．(结果保留π)

【答案】(1)反比例函数的解析式为y＝；(2)S阴影＝6π－.

【解析】分析：（1）根据tan30°=，求出AB，进而求出OA，得出A的坐标，设过A的双曲线的解析式是y=，把A的坐标代入求出即可；（2）求出∠AOA′，根据扇形的面积公式求出扇形AOA′的面积，求出OD、DC长，求出△ODC的面积，相减即可求出答案．

本题解析：

(1)在Rt△OBA中，∠AOB＝30°，OB＝3，

∴AB＝OB·tan 30°＝3.

∴点A的坐标为(3，3)．

设反比例函数的解析式为y＝ (k≠0)，

∴3＝，∴k＝9，则这个反比例函数的解析式为y＝.

(2)在Rt△OBA中，∠AOB＝30°，AB＝3，

sin ∠AOB＝，即sin 30°＝，

∴OA＝6.

由题意得：∠AOC＝60°，S扇形AOA′＝＝6π.

在Rt△OCD中，∠DOC＝45°，OC＝OB＝3，

∴OD＝OC·cos 45°＝3×＝.

∴S△ODC＝OD2＝＝.

∴S阴影＝S扇形AOA′－S△ODC＝6π－.

点睛：本题考查了勾股定理、待定系数法求函数解析式、特殊角的三角函数值、扇形的面积及等腰三角形的性质，本题属于中档题，难度不大，将不规则的图形的面积表示成多个规则图形的面积之和是解答本题的关键.

【题型】解答题
【结束】
26

【题目】矩形ABCD一条边AD＝8，将矩形ABCD折叠，使得点B落在CD边上的点P处．

(1)如图①，已知折痕与边BC交于点O，连接AP，OP，OA.

① 求证：△OCP∽△PDA；

② 若△OCP与△PDA的面积比为1:4，求边AB的长．

(2)如图②，在(1)的条件下，擦去AO和OP，连接BP.动点M在线段AP上(不与点P，A重合)，动点N在线段AB的延长线上，且BN＝PM，连接MN交PB于点F，作ME⊥BP于点E.试问动点M，N在移动的过程中，线段EF的长度是否发生变化？若不变，求出线段EF的长度；若变化，说明理由．

【题目】如图，在等腰中，，点在线段上运动（不与、重合），连接，作，交线段于点.

（1）若，证明：；

（2）在点的运动过程中，的形状可以是等腰三角形吗？若可以，请直接写出的度数；若不可以，请说明理由.

【题目】（本题满分10分）如图，直线y=﹣x+6分别与x轴、y轴交于A、B两点；直线y=x与AB交于点C，与过点A且平行于y轴的直线交于点D．点E从点A出发，以每秒1个单位的速度沿x轴向左运动．过点E作x轴的垂线，分别交直线AB、OD于P、Q两点，以PQ为边向右作正方形PQMN．设正方形PQMN与△ACD重叠部分（阴影部分）的面积为S（平方单位），点E的运动时间为t（秒）．

（1）求点C的坐标．

（2）当0＜t＜5时，求S与t之间的函数关系式，并求S的最大值。

（3）当t＞0时，直接写出点（5，3）在正方形PQMN内部时t的取值范围。

【题目】利用我们学过的知识，可以得出下面这个优美的等式：

；该等式从左到右的变形，不仅保持了结构的对称性，还体现了数学的和谐、简洁美.

⑴.请你证明这个等式；

⑵.如果，请你求出 的值.

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网