题目内容
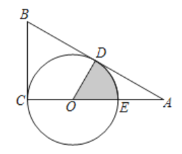
【题目】如图,O为Rt△ABC直角边AC上一点,以OC为半径作⊙O与斜边AB相切于点D,交OA于点E,已知![]() ,AC=3,则图中阴影部分的面积是__________.
,AC=3,则图中阴影部分的面积是__________.
【答案】![]()
【解析】
首先利用勾股定理求出AB的长,再证明BD=BC,进而由AD=AB-BD可求出AD的长度;利用特殊角的锐角三角函数可求出∠A的度数,则圆心角∠DOA的度数可求出,在直角三角形ODA中求出OD的长,最后利用扇形的面积公式即可求出阴影部分的面积.
解:在Rt△ABC中,∵BC=![]() ,AC=3.
,AC=3.
∴AB=![]() =2
=2![]() ,
,
∵BC⊥OC,
∴BC是圆的切线,
∵⊙O与斜边AB相切于点D,
∴BD=BC=![]() ,
,
∴AD=AB-BD=2![]() -
-![]() =
=![]() ;
;
在Rt△ABC中,∵sinA=![]() =
=![]() =
=![]() ,
,
∴∠A=30°,
∵⊙O与斜边AB相切于点D,
∴OD⊥AB,
∴∠AOD=90°-∠A=60°,
∵![]() =tanA=tan30°,
=tanA=tan30°,
∴![]() =
=![]() .
.
∴OD=1,
∴S阴影=![]() =
=![]() .
.
故答案是:![]()

 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案【题目】某工厂生产某种产品,每件产品的出厂价为50元,成本为25元.由于在生产过程中,平均每生产1件产品,有![]() 污水排出,所以为了净化环境,工厂设计两种方案对污水进行处理,并准备实施.
污水排出,所以为了净化环境,工厂设计两种方案对污水进行处理,并准备实施.
方案甲:工厂将污水排到污水厂统一处理,每处理![]() 需付14元的排污费;
需付14元的排污费;
方案乙:工厂将污水进行净化处理后再排出,每处理![]() 污水所用原料费为2元,且每月净化设备的损耗费为30000元.设工厂每月生产x件产品(x为正整数,
污水所用原料费为2元,且每月净化设备的损耗费为30000元.设工厂每月生产x件产品(x为正整数,![]() ).
).
(1)根据题意填写下表:
每月生产产品的数量/件 | 3500 | 4500 | 5500 | … |
方案甲处理污水的费用/元 | 31500 | … | ||
方案乙处理污水的费用/元 | 34500 | … |
(2)设工厂按方案甲处理污水时每月获得的利润为![]() 元,按方案乙处理污水时每月获得的利润为
元,按方案乙处理污水时每月获得的利润为![]() 元,分别求
元,分别求![]() ,
,![]() 关于x的函数解析式;
关于x的函数解析式;
(3)根据题意填空:
①若该工厂按方案甲处理污水时每月获得的利润和按方案乙处理污水时每月获得利润相同,则该工厂每月生产产品的数量为_______件;
②若该工厂每月生产产品的数量为7500件时,则该工厂选用方案甲、方案乙中的方案_______处理污水时所获得的利润多;
③若该工厂每月获得的利润为81000元,则该工厂选用方案甲、方案乙中的方案________处理污水时生产产品的数量少.