题目内容
 如图,正方形ABCD中,E为CD边上一点,F为BC延长线上一点,CE=CF.若∠BEC=80°,则∠EFD的度数为
如图,正方形ABCD中,E为CD边上一点,F为BC延长线上一点,CE=CF.若∠BEC=80°,则∠EFD的度数为
- A.20°
- B.25°
- C.35°
- D.40°
C
分析:根据正方形性质得出BC=CD,∠BCD=∠DCF=90°,根据SAS证△BCE≌△DCF,求出∠DFC=80°,根据等腰直角三角形性质求出∠EFC=45°,即可求出答案.
解答:∵四边形ABCD是正方形,
∴BC=CD,∠BCD=∠DCF=90°,
∵在△BCE和△DCF中
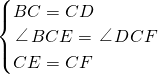 ,
,
∴△BCE≌△DCF,
∴∠DFC=∠BEC=80°,
∵∠DCF=90°,CE=CF,
∴∠CFE=∠CEF=45°,
∴∠EFD=80°-45°=35°.
故选C.
点评:本题考查了等腰直角三角形,全等三角形的性质和判定,正方形的性质的应用,解此题的关键是求出∠DFC的度数,主要培养学生运用性质进行推理的能力,全等三角形的对应角相等,等腰直角三角形的两锐角的度数是45°.
分析:根据正方形性质得出BC=CD,∠BCD=∠DCF=90°,根据SAS证△BCE≌△DCF,求出∠DFC=80°,根据等腰直角三角形性质求出∠EFC=45°,即可求出答案.
解答:∵四边形ABCD是正方形,
∴BC=CD,∠BCD=∠DCF=90°,
∵在△BCE和△DCF中
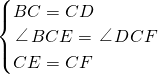 ,
,∴△BCE≌△DCF,
∴∠DFC=∠BEC=80°,
∵∠DCF=90°,CE=CF,
∴∠CFE=∠CEF=45°,
∴∠EFD=80°-45°=35°.
故选C.
点评:本题考查了等腰直角三角形,全等三角形的性质和判定,正方形的性质的应用,解此题的关键是求出∠DFC的度数,主要培养学生运用性质进行推理的能力,全等三角形的对应角相等,等腰直角三角形的两锐角的度数是45°.

练习册系列答案
相关题目
 19、如图:正方形ABCD,M是线段BC上一点,且不与B、C重合,AE⊥DM于E,CF⊥DM于F.求证:AE2+CF2=AD2.
19、如图:正方形ABCD,M是线段BC上一点,且不与B、C重合,AE⊥DM于E,CF⊥DM于F.求证:AE2+CF2=AD2. 如图,正方形ABCD中,E点在BC上,AE平分∠BAC.若BE=
如图,正方形ABCD中,E点在BC上,AE平分∠BAC.若BE= 如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF.下列结论:①△ABG≌△AFG;②BG=GC;③AG∥CF;④S△FGC=3.其中正确结论的个数是( )
如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF.下列结论:①△ABG≌△AFG;②BG=GC;③AG∥CF;④S△FGC=3.其中正确结论的个数是( ) 17、如图,正方形ABCD的边长为4,将一个足够大的直角三角板的直角顶点放于点A处,该三角板的两条直角边与CD交于点F,与CB延长线交于点E,四边形AECF的面积是
17、如图,正方形ABCD的边长为4,将一个足够大的直角三角板的直角顶点放于点A处,该三角板的两条直角边与CD交于点F,与CB延长线交于点E,四边形AECF的面积是 如图,正方形ABCD的边CD在正方形ECGF的边CE上,连接BE、DG.
如图,正方形ABCD的边CD在正方形ECGF的边CE上,连接BE、DG.