题目内容
【题目】以直线![]() 上点
上点![]() 为端点作射线
为端点作射线![]() ,使
,使![]() ,将直角
,将直角![]() 的直角顶点放在点
的直角顶点放在点![]() 处.
处.
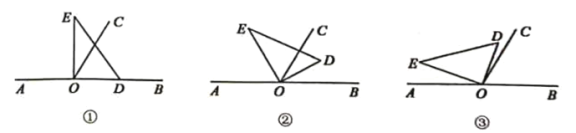
(1)若直角![]() 的边
的边![]() 在射线
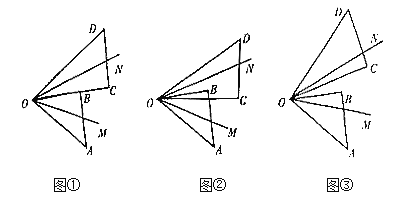
在射线![]() 上(图①),求
上(图①),求![]() 的度数;
的度数;
(2)将直角![]() 绕点
绕点![]() 按逆时针方向转动,使得
按逆时针方向转动,使得![]() 所在射线平分
所在射线平分![]() (图②),说明
(图②),说明![]() 所在射线是
所在射线是![]() 的平分线;
的平分线;
(3)将直角![]() 绕点
绕点![]() 按逆时针方向转动到某个位置时,恰好使得
按逆时针方向转动到某个位置时,恰好使得![]() (图③),求
(图③),求![]() 的度数.
的度数.
【答案】(1)![]() ;(2)见解析; (3)
;(2)见解析; (3) ![]() 或
或![]()
【解析】
(1)代入∠BOE=∠COE+∠COB求出即可;
(2)求出∠AOE=∠COE,根据∠DOE=90°求出∠AOE+∠DOB=90°,∠COE+∠COD=90°,推出∠COD=∠DOB,即可得出答案;
(3)要分情况讨论,一种是∠COD在∠BOC的内部,另一种是∠COD在∠BOC的外部,再根据平角等于180°可通过列方程求出即可.
解:(1)∵![]() ,
,
又∵![]() ,
,
∴![]() .
.
(2)∵![]() 平分
平分![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() 所在直线是
所在直线是![]() 的平分线.
的平分线.
(3)设![]() ,则
,则![]() ,
,
∵![]() ,
,![]() ,
,
①若∠COD在∠BOC的外部,
∴![]() ,解得x=10,
,解得x=10,
∴∠COD=10°,
∴∠BOD=60°+10°=70°;
②若∠COD在∠BOC的内部,
![]() ,解得x=30,
,解得x=30,
∴∠COD=30°,
∴∠BOD=60°-30°=30°;
即![]() 或
或![]() ,
,
∴![]() 或
或![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目