题目内容
(1)已知菱形ABCD的边长为6,∠A=60°,如果点P是菱形内一点,且PB=PD=2
,那么AP的长为 .
(2)对于任意实数x,二次三项式x2+3mx+m2-m+
是一个完全平方式,则m= .
| 3 |
(2)对于任意实数x,二次三项式x2+3mx+m2-m+
| 1 |
| 4 |
考点:菱形的性质,完全平方式
专题:
分析:(1)根据题意得,应分P与A在BD的同侧与异侧两种情况进行讨论;
(2)根据完全平方公式的定义,a2±2ab+b2=(a±b)2,解出即可;
(2)根据完全平方公式的定义,a2±2ab+b2=(a±b)2,解出即可;
解答:解:(1)当P与A在BD的异侧时:连接AP交BD于M,
∵AD=AB,DP=BP,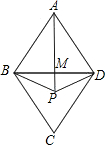
∴AP⊥BD(到线段两端距离相等的点在垂直平分线上),
在直角△ABM中,∠BAM=30°,
∴AM=AB•cos30°=3
,BM=AB•sin30°=3,
∴PM=
,
∴AP=AM+PM=4
;
当P与A在BD的同侧时:连接AP并延长AP交BD于点M
AP=AM-PM=2
;
当P与M重合时,PD=PB=3,与PB=PD=2
矛盾,舍去.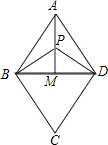
AP的长为4
或2
.
故答案为:4
或2
.
(2)二次三项式x2+3mx+m2-m+
是一个完全平方式,
∴x2+3mx+m2-m+
=(x+
)2-
m2-m+
,
∴-
m2-m+
=0,
解得:m=-1或5.
故答案为:-1或5.
∵AD=AB,DP=BP,
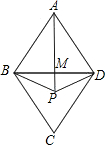
∴AP⊥BD(到线段两端距离相等的点在垂直平分线上),
在直角△ABM中,∠BAM=30°,
∴AM=AB•cos30°=3
| 3 |
∴PM=
| 3 |
∴AP=AM+PM=4
| 3 |
当P与A在BD的同侧时:连接AP并延长AP交BD于点M
AP=AM-PM=2
| 3 |
当P与M重合时,PD=PB=3,与PB=PD=2
| 3 |

AP的长为4
| 3 |
| 3 |
故答案为:4
| 3 |
| 3 |
(2)二次三项式x2+3mx+m2-m+
| 1 |
| 4 |
∴x2+3mx+m2-m+
| 1 |
| 4 |
| 3m |
| 2 |
| 5 |
| 4 |
| 1 |
| 4 |
∴-
| 5 |
| 4 |
| 1 |
| 4 |
解得:m=-1或5.
故答案为:-1或5.
点评:本题考查了完全平方公式以及菱形的性质,注意分两种情况讨论,并且注意两种情况都存在关系AP⊥BD,这是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
sin27°=( )
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
 如图,将线段OA绕点O顺时针方向旋转90°,则点A(-4,3)对应的坐标为( )
如图,将线段OA绕点O顺时针方向旋转90°,则点A(-4,3)对应的坐标为( )| A、(-3,-4) |
| B、(3,4) |
| C、(4,3) |
| D、(-4,-3) |
抛物线y=(x-2)2+3的顶点在( )
| A、第一象限 | B、第二象限 |
| C、x轴上 | D、y轴上 |
 如图所示,有一名民警在值班,他位于到平行的大街两侧以及过街天桥AB的距离相等的点P处.此时,这位民警发现有一可疑分子从天桥A处走向B处,请问民警在注视可疑分子从A处走到B处时,他的视线转过了
如图所示,有一名民警在值班,他位于到平行的大街两侧以及过街天桥AB的距离相等的点P处.此时,这位民警发现有一可疑分子从天桥A处走向B处,请问民警在注视可疑分子从A处走到B处时,他的视线转过了