题目内容
 如图,抛物线y=
如图,抛物线y=
| ||
| 9 |
(1)求该抛物线的解析式和点D的坐标;
(2)点E(x,0)是线段OB上的动点,过点E作EP∥BD,交OD于点P,连接DE.△PED的面积为S,求S与x的函数关系式,并求当x为何值时,S最大;
(3)在抛物线是否存在一点Q,使以点B、D、E、Q为顶点的四边形为平行四边形?若存在,请求出所有符合条件的Q点的坐标和此时x的值;若不存在,请说明理由.
分析:(1)把点A、B的坐标代入抛物线解析式,利用待定系数法求二次函数解析式解答即可;再把抛物线解析式整理成顶点式形式,然后写出顶点D的坐标;
(2)根据点B、D的坐标求出OD、BD的长度,再利用勾股定理逆定理求出∠ODB=90°,然后判断出△OPE和△ODB相似,根据相似三角形对应边成比例列出比例式用x表示出OP、PE,再求出PD,再根据∠EPD=90°,然后利用三角形的面积公式列式整理即可得到S与x的函数关系式,最后根据二次函数的最值问题解答即可;
(3)分①BD为平行四边形的对角线,D、Q重合,不合题意,②ED为平行四边形的对角线,D、Q重合,不合题意,③BE为平行四边形的对角线,作DF⊥x轴于F,作QG⊥x轴于G,可以判定△DFE和△QGB全等,根据全等三角形对应边相等可得QG=DF=
,然后代入抛物线解析式求出点Q的横坐标,从而得到点Q的坐标,再求出EF的长,然后根据x=OF+EF,代入数据进行计算即可得解.
(2)根据点B、D的坐标求出OD、BD的长度,再利用勾股定理逆定理求出∠ODB=90°,然后判断出△OPE和△ODB相似,根据相似三角形对应边成比例列出比例式用x表示出OP、PE,再求出PD,再根据∠EPD=90°,然后利用三角形的面积公式列式整理即可得到S与x的函数关系式,最后根据二次函数的最值问题解答即可;
(3)分①BD为平行四边形的对角线,D、Q重合,不合题意,②ED为平行四边形的对角线,D、Q重合,不合题意,③BE为平行四边形的对角线,作DF⊥x轴于F,作QG⊥x轴于G,可以判定△DFE和△QGB全等,根据全等三角形对应边相等可得QG=DF=
| 3 |
解答:解:(1)∵抛物线y=
x2+ax+c(a≠0)与x轴交于点A(-2,0),B(4,0),
∴
,
解得
,
所以抛物线的解析式为y=
x2-
x-
;
∵y=
x2-
x-
=
(x-1)2-
,
∴顶点D的坐标(1,-
);
(2)∵B(4,0),D(1,-
),
∴OB=4,OD=
=2,BD=
=2
,
∴OD2+BD2=OB2=16,
∴∠ODB=90°,
∵EP∥BD,
∴△OPE∽△ODB,
∴
=
=
,
即
=
=
,
解得OP=
x,PE=
x,
∴PD=OD-OP=2-
x,
又∵EP∥BD,
∴∠EPD=180°-∠ODB=180°-90°=90°,
S=
×(2-
x)×
x=-
x2+
x,
即S=-
x2+
x,
∵S=-
x2+
x=-
(x-2)2+
,
∴当x为2时,S最大;
(3)以点B、D、E、Q为顶点的四边形为平行四边形分三种情况,
①BD为平行四边形的对角线,BE∥DQ,即DQ∥x轴,
所以,直线DQ与抛物线只有一个交点D,Q与D重合,不合题意;
②ED为平行四边形的对角线,BE∥DQ,即DQ∥x轴,
所以,直线DQ与抛物线只有一个交点D,Q与D重合,不合题意;
③BE为平行四边形的对角线,如图,作DF⊥x轴于F,作QG⊥x轴于G,
∵四边形DBQE为平行四边形,
∴DE∥BQ,DE=QB,
∴∠BED=∠EBQ,
∴∠DEF=∠QBG,
∵在△DFE和△QGB中,
,
∴△DFE≌△QGB(AAS),
∴QG=DF=
,
当y=
时,
x2-
x-
=
,
整理得,x2-2x-17=0,
解得x1=1+3
,x2=1-3
(是负数,舍去),
∴点Q(1+3
,
),
∴EF=BG=1+3
-4=3
-3,
x=OE=OF+EF=1+(3
-3)=3
-2,
∴存在Q(1+3
,
),使以点B、D、E、Q为顶点的四边形为平行四边形,此时x=3
-2.
| ||
| 9 |
∴
|
解得
|
所以抛物线的解析式为y=
| ||
| 9 |
2
| ||
| 9 |
8
| ||
| 9 |
∵y=
| ||
| 9 |
2
| ||
| 9 |
8
| ||
| 9 |
| ||
| 9 |
| 3 |
∴顶点D的坐标(1,-
| 3 |
(2)∵B(4,0),D(1,-
| 3 |
∴OB=4,OD=
12+
|
|
| 3 |
∴OD2+BD2=OB2=16,
∴∠ODB=90°,
∵EP∥BD,
∴△OPE∽△ODB,
∴
| OE |
| OB |
| OP |
| OD |
| PE |
| BD |
即
| x |
| 4 |
| OP |
| 2 |
| PE | ||
2
|
解得OP=
| 1 |
| 2 |
| ||
| 2 |
∴PD=OD-OP=2-
| 1 |
| 2 |
又∵EP∥BD,
∴∠EPD=180°-∠ODB=180°-90°=90°,
S=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 8 |
| ||
| 2 |
即S=-
| ||
| 8 |
| ||
| 2 |
∵S=-
| ||
| 8 |
| ||
| 2 |
| ||
| 8 |
| ||
| 2 |
∴当x为2时,S最大;
(3)以点B、D、E、Q为顶点的四边形为平行四边形分三种情况,
①BD为平行四边形的对角线,BE∥DQ,即DQ∥x轴,
所以,直线DQ与抛物线只有一个交点D,Q与D重合,不合题意;
②ED为平行四边形的对角线,BE∥DQ,即DQ∥x轴,
所以,直线DQ与抛物线只有一个交点D,Q与D重合,不合题意;
③BE为平行四边形的对角线,如图,作DF⊥x轴于F,作QG⊥x轴于G,

∵四边形DBQE为平行四边形,
∴DE∥BQ,DE=QB,
∴∠BED=∠EBQ,
∴∠DEF=∠QBG,
∵在△DFE和△QGB中,
|
∴△DFE≌△QGB(AAS),
∴QG=DF=
| 3 |
当y=
| 3 |
| ||
| 9 |
2
| ||
| 9 |
8
| ||
| 9 |
| 3 |
整理得,x2-2x-17=0,
解得x1=1+3
| 2 |
| 2 |
∴点Q(1+3
| 2 |
| 3 |
∴EF=BG=1+3
| 2 |
| 2 |
x=OE=OF+EF=1+(3
| 2 |
| 2 |
∴存在Q(1+3
| 2 |
| 3 |
| 2 |
点评:本题是二次函数综合题型,主要考查了待定系数法求二次函数解析式,主要考查了二次函数的顶点坐标的求解,勾股定理的应用,勾股定理逆定理的应用,相似三角形的判定与性质,全等三角形的判定与性质,二次函数的最值问题,以及平行四边形的性质,综合性较强,难度较大,(3)要分情况讨论.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
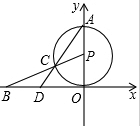 如图,⊙P与x轴相切于坐标原点O,点A(0,2)是⊙P与y轴的交点,点B(
如图,⊙P与x轴相切于坐标原点O,点A(0,2)是⊙P与y轴的交点,点B(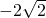 ,0)在x轴上,连接BP交⊙P于点C,连接AC并延长交x轴于点D.
,0)在x轴上,连接BP交⊙P于点C,连接AC并延长交x轴于点D. 如图,在直角坐标系中,y轴是边长为2的等边△BAD的对称轴,x轴是等腰△BDC的对称轴.
如图,在直角坐标系中,y轴是边长为2的等边△BAD的对称轴,x轴是等腰△BDC的对称轴.