Question

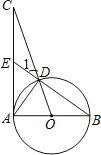
【题目】如图，四边形ABCD 中，AB=AD，点B关于AC的对称点B′恰好落在CD上，若∠BAD=，则∠ACB的度数为（　　）

A. α B. 90°-α C. 45° D. α-45°

Answer 1

【答案】B

【解析】

连接AB'，BB'，过A作AE⊥CD于E，依据∠BAC=∠B'AC，∠DAE=∠B'AE，即可得出∠CAE=∠BAD=，再根据四边形内角和以及三角形外角性质，即可得到∠ACB=∠ACB'=90°﹣．

如图，连接AB'，BB'，过A作AE⊥CD于E．

∵点B关于AC的对称点B'恰好落在CD上，∴AC垂直平分BB'，∴AB=AB'，∴∠BAC=∠B'AC．

∵AB=AD，∴AD=AB'．

又∵AE⊥CD，∴∠DAE=∠B'AE，∴∠CAE=∠BAD=．

又∵∠AEB'=∠AOB'=90°，∴四边形AOB'E中，∠EB'O=180°﹣，∴∠ACB'=∠EB'O﹣∠COB'=180°﹣﹣90°=90°﹣，∴∠ACB=∠ACB'=90°﹣．

故选B．