题目内容
已知关于x的一元二次方程(6-k)(9-k)x2-(117-15k)x+54=0的两个根均为整数,求所有满足条件的实数k的值.
解:原方程可化为:[(6-k)x-9][(9-k)x-6]=0.
因为此方程是关于x的一元二次方程,
所以,k≠6,k≠9,
于是有:x1= ①,x2=
①,x2= ②.
②.
由①得k= ,由②得k=
,由②得k= ,
,
∴ =
= ,
,
整理得x1x2-2x1+3x2=0,
有(x1+3)(x2-2)=-6.
∵x1、x2均为整数,
∴ .
.
故x1=-9,-6,-5,-4,-2,-1,0,3.
又k= =6-
=6- ,
,
将x1=-9,-6,-5,-4,-2,-1,3分别代入,得
k=7, ,
, ,
,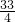 ,
, ,15,3.
,15,3.
分析:首先对方程(6-k)(9-k)x2-(117-15k)x+54=0因式分解可得[(6-k)x-9][(9-k)x-6]=0,于是有x1= ,x2=
,x2= .消去k后,有(x1+3)(x2-2)=-6,列出所有x1、x2对应的整数,即可求得对应的k的值.
.消去k后,有(x1+3)(x2-2)=-6,列出所有x1、x2对应的整数,即可求得对应的k的值.
点评:正确利用因式分解法求得方程的解,得到方程的两个解之间的关系(x1+3)(x2-2)=-6,根据x1、x2均为整数,确定x的取值是解决本题的关键.
因为此方程是关于x的一元二次方程,
所以,k≠6,k≠9,
于是有:x1=
 ①,x2=
①,x2= ②.
②.由①得k=
 ,由②得k=
,由②得k= ,
,∴
 =
= ,
,整理得x1x2-2x1+3x2=0,
有(x1+3)(x2-2)=-6.
∵x1、x2均为整数,
∴
 .
.故x1=-9,-6,-5,-4,-2,-1,0,3.
又k=
 =6-
=6- ,
,将x1=-9,-6,-5,-4,-2,-1,3分别代入,得
k=7,
 ,
, ,
,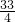 ,
, ,15,3.
,15,3.分析:首先对方程(6-k)(9-k)x2-(117-15k)x+54=0因式分解可得[(6-k)x-9][(9-k)x-6]=0,于是有x1=
 ,x2=
,x2= .消去k后,有(x1+3)(x2-2)=-6,列出所有x1、x2对应的整数,即可求得对应的k的值.
.消去k后,有(x1+3)(x2-2)=-6,列出所有x1、x2对应的整数,即可求得对应的k的值.点评:正确利用因式分解法求得方程的解,得到方程的两个解之间的关系(x1+3)(x2-2)=-6,根据x1、x2均为整数,确定x的取值是解决本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知关于x的一元二次x2-6x+k+1=0的两个实数根x1,x2,
+
=1,则k的值是( )
| 1 |
| x1 |
| 1 |
| x2 |
| A、8 | B、-7 | C、6 | D、5 |
 .
. .
.