题目内容
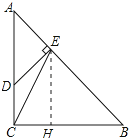
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=BC=3,点D在边AC上,且AD=2CD,DE⊥AB,垂足为点E,联结CE,求: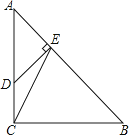
(1)线段BE的长;
(2)∠ECB的余切值.
【答案】
(1)
解:∵AD=2CD,AC=3,
∴AD=2,
∵在Rt△ABC中,∠ACB=90°,AC=BC=3,
∴∠A=∠B=45°,AB= ![]() =
= ![]() =3
=3 ![]() ,
,
∵DE⊥AB,
∴∠AED=90°,∠ADE=∠A=45°,
∴AE=ADcos45°=2× ![]() =
= ![]() ,
,
∴BE=AB﹣AE=3 ![]() ﹣
﹣ ![]() =2
=2 ![]() ,
,
即线段BE的长为2 ![]()
(2)
解:过点E作EH⊥BC,垂足为点H,如图所示:
∵在Rt△BEH中,∠EHB=90°,∠B=45°,
∴EH=BH=BEcos45°=2 ![]() ×
× ![]() =2,
=2,
∵BC=3,
∴CH=1,
在Rt△CHE中,cot∠ECB= ![]() =
= ![]() ,
,
即∠ECB的余切值为 ![]()
【解析】(1)由等腰直角三角形的性质得出∠A=∠B=45°,由勾股定理求出AB=3 ![]() ,求出∠ADE=∠A=45°,由三角函数得出AE=
,求出∠ADE=∠A=45°,由三角函数得出AE= ![]() ,即可得出BE的长;(2)过点E作EH⊥BC,垂足为点H,由三角函数求出EH=BH=BEcos45°=2,得出CH=1,在Rt△CHE中,由三角函数求出cot∠ECB=
,即可得出BE的长;(2)过点E作EH⊥BC,垂足为点H,由三角函数求出EH=BH=BEcos45°=2,得出CH=1,在Rt△CHE中,由三角函数求出cot∠ECB= ![]() 即可.本题考查了解直角三角形、勾股定理、等腰直角三角形的性质、三角函数;熟练掌握等腰直角三角形的性质,通过作辅助线求出CH是解决问题(2)的关键.
即可.本题考查了解直角三角形、勾股定理、等腰直角三角形的性质、三角函数;熟练掌握等腰直角三角形的性质,通过作辅助线求出CH是解决问题(2)的关键.

 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案【题目】抛物线y=﹣x2+bx+c上部分点的横坐标x,纵坐标y的对应值如表:
x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | … |
y | … | 0 | 4 | 6 | 6 | 4 | … |
从上表可知,有下列说法:
①抛物线与y轴的交点为(0,6);
②抛物线的对称轴是x=1;
③抛物线与x轴有两个交点,它们之间的距离是 ![]() ;
;
④在对称轴左侧y随x增大而增大.
其中正确的说法是( )
A.①②③
B.②③④
C.②③
D.①④