题目内容
在等腰梯形ABCD中，AD∥BC，AB=AD=CD=8cm，∠C=60°，则梯形ABCD的周长为________．
40cm
分析：作DE∥AB交BC与点E．则四边形ABED是平行四边形，△DEC是等边三角形，即可求得CD，BE的长度，从而求解．
解答：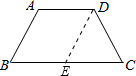
作DE∥AB交BC与点E．
∵AD∥BC，DE∥AB，
∴四边形ABED是平行四边形，
∴AB=AD=CD=DE=BE=8cm，
∵∠C=60°，
∴△DEC是等边三角形．
∴EC=DC=AB=8cm．
∴梯形ABCD的周长=AD+AB+BC+CD=AB+AD+BE+EC+CD=8×5=40cm．
故答案为：40cm．
点评：本题考查等腰梯形的性质，正确作出辅助线，把等腰梯形转化成平行四边形与等边三角形是解答此题的关键．
分析：作DE∥AB交BC与点E．则四边形ABED是平行四边形，△DEC是等边三角形，即可求得CD，BE的长度，从而求解．
解答：
作DE∥AB交BC与点E．∵AD∥BC，DE∥AB，
∴四边形ABED是平行四边形，
∴AB=AD=CD=DE=BE=8cm，
∵∠C=60°，
∴△DEC是等边三角形．
∴EC=DC=AB=8cm．
∴梯形ABCD的周长=AD+AB+BC+CD=AB+AD+BE+EC+CD=8×5=40cm．
故答案为：40cm．
点评：本题考查等腰梯形的性质，正确作出辅助线，把等腰梯形转化成平行四边形与等边三角形是解答此题的关键．
练习册系列答案
王后雄学案教材完全解读系列答案
海淀课时新作业金榜卷系列答案
相关题目
25、如图所示，在等腰梯形ABCD中，AD∥BC，AB=CD，点P为BC边上任意一点，且
24、已知：如图，在等腰梯形ABCD中，AD∥BC，AB=DC，点E为边BC上一点，且AE=DC．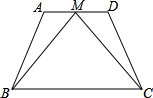
如图，在等腰梯形ABCD中，AD∥BC，M是AD的中点，MB=MC吗？为什么？
如图，在等腰梯形ABCD中，AD∥BC，AB=CD，AC⊥BD，垂足为O，过D作DE∥AC交BC的延长线于E．