题目内容
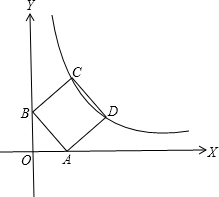 已知如图正方形ABCD的C、D的两个顶点在双曲线y=
已知如图正方形ABCD的C、D的两个顶点在双曲线y=| 10 | x |
分析:连接BD,过点D作DE⊥OA于E,作CF⊥y轴.可以证明,△ABO≌△DAE≌△BCF,即可表示出C,D的坐标,即可证得△ABO是等腰直角三角形,再根据D在函数的图象上,即可求解.
解答: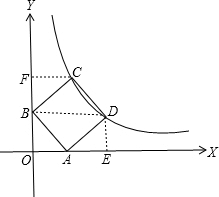 解:连接BD,过点D作DE⊥OA于E,作CF⊥y轴.
解:连接BD,过点D作DE⊥OA于E,作CF⊥y轴.
∴∠DEA=90°,
∵四边形ABCD是正方形,
∴AB=AD,∠BAD=90°,
∴∠BAO+∠DAE=90°,∠DAE+∠ADE=90°,
∴∠DAE=∠ABO,
又∵AB=AD,
∴△ABO≌△DAE.
同理,△ABO≌△BCF.
设OA=a,AE=b,则OB=b,BF=a,DE=a,CF=b.
则D的坐标是(a+b,a),C的坐标是(b,a+b).
∵C、D的两个顶点在双曲线y=
的第一象限分支上.
∴a(a+b)=b(a+b)=10,
∴a=b,即△ABO是等腰直角三角形.
则D的坐标是(2a,a)代入函数解析式得:2a2=10
∴a2=5,
∴OB2+OA2=10,
则AB=
故答案是
.
 解:连接BD,过点D作DE⊥OA于E,作CF⊥y轴.
解:连接BD,过点D作DE⊥OA于E,作CF⊥y轴.∴∠DEA=90°,
∵四边形ABCD是正方形,
∴AB=AD,∠BAD=90°,
∴∠BAO+∠DAE=90°,∠DAE+∠ADE=90°,
∴∠DAE=∠ABO,
又∵AB=AD,
∴△ABO≌△DAE.
同理,△ABO≌△BCF.
设OA=a,AE=b,则OB=b,BF=a,DE=a,CF=b.
则D的坐标是(a+b,a),C的坐标是(b,a+b).
∵C、D的两个顶点在双曲线y=
| 10 |
| x |
∴a(a+b)=b(a+b)=10,
∴a=b,即△ABO是等腰直角三角形.
则D的坐标是(2a,a)代入函数解析式得:2a2=10
∴a2=5,
∴OB2+OA2=10,
则AB=
| 10 |
故答案是
| 10 |
点评:本题主要考查反比例函数的性质,注意通过解方程组求出交点坐标.同时要注意运用数形结合的思想.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
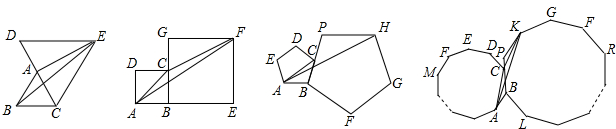

 ,四边形ABCD和四边形BEFG都是正方形,若正方形ABCD的边长为4,则△FAC的面积是8,……,如果两个正多边形ABCDE…和BPKGY…是正n(n≥3)边形,正多边形ABCDE …的边长是2a,则△KCA的面积是 .(结果用含有a、n的代数式表示)
,四边形ABCD和四边形BEFG都是正方形,若正方形ABCD的边长为4,则△FAC的面积是8,……,如果两个正多边形ABCDE…和BPKGY…是正n(n≥3)边形,正多边形ABCDE …的边长是2a,则△KCA的面积是 .(结果用含有a、n的代数式表示)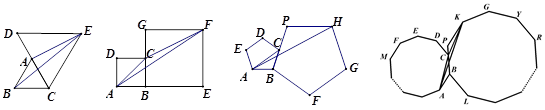
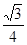 ,四边形ABCD和四边形BEFG都是正方形,若正方形ABCD的边长为4,则△FAC的面积是8,……,如果两个正多边形ABCDE…和BPKGY…是正n(n≥3)边形,正多边形ABCDE …的边长是2a,则△KCA的面积是 .(结果用含有a、n的代数式表示)
,四边形ABCD和四边形BEFG都是正方形,若正方形ABCD的边长为4,则△FAC的面积是8,……,如果两个正多边形ABCDE…和BPKGY…是正n(n≥3)边形,正多边形ABCDE …的边长是2a,则△KCA的面积是 .(结果用含有a、n的代数式表示)
