题目内容
【题目】如图,已知A,F,E,C在同一直线上,AB∥CD,∠1=∠2,AF=CE.
(1)写出图中全等的三角形;
(2)选择其中一对,说明理由.
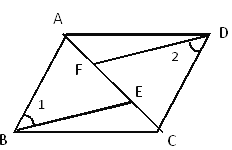
【答案】(1)△ABE≌△CDF,△ADF≌△CBE,△ABC≌△CDA;(2)证明见解析.
【解析】试题解析:(1)根据条件可得∠BAC=∠DCA,AE=CF,加上∠1=∠2可证明△ABE≌△CDF,进而可得AB=CD,可利用SAS判定△ABC≌△CDA,可得BC=AD,∠DAF=∠FCD,然后可得△AFD≌△CEB;
(2)根据条件AB∥CD可得∠BAC=∠DCA,根据等式的性质可得AE=CF,加上∠1=∠2可证明△ABE≌△CDF.
试题解析:(1)△ABE≌△CDF,△ADF≌△CBE,△ABC≌△CDA
(2)∵ AB∥CD,
∴ ∠BAC=∠DCA,
∵ AF=CE,
∴ AF+EF=CE+EF,
即AE=CF,
∵ ∠1=∠2,
∴ △ABE≌△CDF(AAS)

练习册系列答案
相关题目