题目内容
解方程组:
(1) ;
;
(2) .
.
(3) ;
;
(4) .
.
解:(1)在 中,
中,
①×2-②得:7y=35,
解得y=5,
代入①得:2x+25=25,
解得x=0.
∴原方程组的解为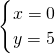 .
.
(2)在 中,
中,
②×6-①得:2x-1=0,
x= ,
,
代入①得: +1=2y,
+1=2y,
y= .
.
原方程组的解为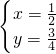 .
.
(3)在 中,
中,
可化为 ,
,
①×9-②得:x=2000,
代入①得:y=1500.
原方程组的解为 .
.
(4)原方程组 可化为
可化为 ,
,
①×13+②×5得:x=4,
代入①得y=4.
原方程组的解为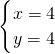 .
.
分析:根据各方程组的特点采用相应的方法求解.
点评:解答此类题目关键是要注意观察各方乘组的特点,采用相应的方法,含分母的应先去分母,去括号,移项,把各方乘化成最简形式,对三元一次方程组要先化成二元一次方程组求解.
 中,
中,①×2-②得:7y=35,
解得y=5,
代入①得:2x+25=25,
解得x=0.
∴原方程组的解为
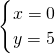 .
.(2)在
 中,
中,②×6-①得:2x-1=0,
x=
 ,
,代入①得:
 +1=2y,
+1=2y,y=
 .
.原方程组的解为
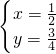 .
.(3)在
 中,
中,可化为
 ,
,①×9-②得:x=2000,
代入①得:y=1500.
原方程组的解为
 .
.(4)原方程组
 可化为
可化为 ,
,①×13+②×5得:x=4,
代入①得y=4.
原方程组的解为
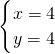 .
.分析:根据各方程组的特点采用相应的方法求解.
点评:解答此类题目关键是要注意观察各方乘组的特点,采用相应的方法,含分母的应先去分母,去括号,移项,把各方乘化成最简形式,对三元一次方程组要先化成二元一次方程组求解.

练习册系列答案
相关题目
 (1)解方程组:
(1)解方程组: