Question

如图：（1）画△ABC的外角∠CAD，再画∠CAD的平分线AE；
（2）已知：△ABC中，∠B=∠C，AE是外角∠CAD的平分线．请说明：AE∥BC．

Answer 1

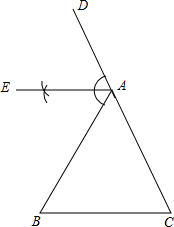解：（1）如图．

（2）证明：
∵∠C=∠B，∠CAD是△ABC的外角，
∴∠DAB=∠C+∠B=2∠B，
∵AE是外角∠CAD的平分线，
∴∠EAB=∠DAB=×2∠B=∠B，
∴AE∥BC（内错角相等，两直线平行）
分析：如答图所示，要证明两直线平行，只需证内错角∠B=∠EAB即可．
点评：本题考查的是角平分线的作法和平行线的性质．