Question

有一个截面边缘为抛物线形的拱形桥洞，桥洞离水面的最大高度为4m，跨度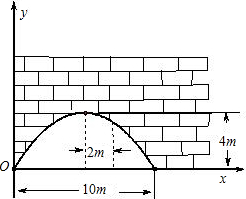为10m．把它的截面边缘的图形放在如图所示的直角坐标系中．
（1）直接写出抛物线的顶点坐标；
（2）求这条抛物线所对应的函数关系式；
（3）如图，在对称轴右边2m处，桥洞离水面的高是多少？

Answer 1

分析：（1）由图象可知抛物线的顶点坐标，
（2）设这条抛物线所对应的函数关系式为y=a（x-5）²+4，经过原点，求得a，
（3）知道函数关系式，令x=7，求y．

解答：解：由题意得：
（1）抛物线的顶点坐标为（5，4）；（2分）

（2）设这条抛物线所对应的函数关系式为y=a（x-5）²+4；（3分）
因为图象经过（0，0），
所以0=25a+4（4分）
解得a=-

4

25

（5分）
函数关系式为：y=-

4

25

(x-5)2+4=-

4

25

x²+

8

5

x；（6分）

（3）如图，当x=7时，桥洞离水面的高度为y=-

4

25

(7-5)2+4=3

9

25

．（8分）

点评：本题主要考查二次函数的应用，本题运用二次函数的顶点坐标式，运用二次函数解决实际问题，比较简单．